题目内容
设M={x|-2≤x≤2},N={y|0≤y≤2},函数f(x)的定义域为M,值域为N,则f(x)的图象可以是( )
B
解析试题分析:根据函数的定义可知一个x只能对应一个y,可排除C,然后再根据-2≤x≤2,排除A,然后再根据0≤y≤2,排除D,故选B
考点:本题考查了函数的概念
点评:函数中的对应常见由一对一或者多对一,另外函数的值域就是y的所有范围。

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
设 ,函数
,函数 的导函数是
的导函数是 ,且
,且 是奇函数,则
是奇函数,则 的值为
的值为
A. | B. | C. | D. |
函数 ,则函数
,则函数 的定义域为
的定义域为
A. | B. | C. | D. |
函数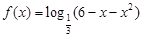 的单调递增区间是
的单调递增区间是
A. | B. | C. | D. |
设 是连续的偶函数,且当
是连续的偶函数,且当 时
时 是单调函数,则满足
是单调函数,则满足 的所有
的所有 之和为( )
之和为( )
A. | B. | C.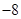 | D. |
已知函数 的定义域为R,当
的定义域为R,当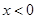 时,
时, ,且对任意的实数
,且对任意的实数 R,等式
R,等式 成立.若数列
成立.若数列 满足
满足 ,且
,且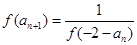 (
( ),则
),则 的值为( )
的值为( )
| A.4024 | B.4023 | C.4022 | D.4021 |
函数 的零点所在的区间是( )
的零点所在的区间是( )
A. | B. | C. | D. |
 的函数
的函数 ,若存在非零实数
,若存在非零实数 ,使函数
,使函数 和
和 上均有零点,则称
上均有零点,则称



 其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:①若P∩M=
其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:①若P∩M=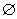 ,则f(P)∩f(M)=
,则f(P)∩f(M)=