题目内容
若函数 的零点与
的零点与 的零点之差的绝对值不超过
的零点之差的绝对值不超过 ,则
,则 可以是
可以是
A. | B. |
C. | D. |
A
解析试题分析:∵ 在R上连续,且g(
在R上连续,且g( )=
)=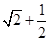 -2=
-2=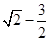 <0,g(
<0,g( )=2+1-2=1>0.
)=2+1-2=1>0.
设g(x)=4x+2x-2的零点为x0,则x0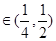
又f(x)=4x-1零点为x= ;f(x)=(x-1)2的零点为x=1;
;f(x)=(x-1)2的零点为x=1;
f(x)=ex-1零点为x=0;f(x)=ln(x- )零点为x=
)零点为x=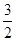 ,
,
∴|x0- |<
|< ,即A中的函数符合题意,故选A.
,即A中的函数符合题意,故选A.
考点:本题主要考查函数零点的概念,函数零点存在定理。
点评:简单题,利用零点存在判定定理,确定得到g(x)零点的存在范围,通过求几个常见函数的零点,比对,作出判断。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数 的定义域为R,当
的定义域为R,当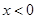 时,
时, ,且对任意的实数
,且对任意的实数 R,等式
R,等式 成立.若数列
成立.若数列 满足
满足 ,且
,且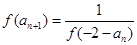 (
( ),则
),则 的值为( )
的值为( )
| A.4024 | B.4023 | C.4022 | D.4021 |
函数 的零点所在的区间是( )
的零点所在的区间是( )
A. | B. | C. | D. |
若定义 上的函数
上的函数 满足:对于任意
满足:对于任意

 且当
且当 时有
时有 ,若
,若 的最大值、最小值分别为M,N,M+N等于( )
的最大值、最小值分别为M,N,M+N等于( )
| A.2011 | B.2012 | C.4022 | D.4024 |
已知 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时
时 的图像如图,那么不等式
的图像如图,那么不等式 的解集是
的解集是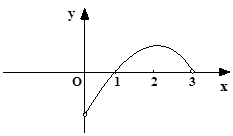
A. | B. |
C. | D. |
已知函数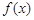 满足:①定义域为R;②
满足:①定义域为R;② ,有
,有 ;③当
;③当 时,
时, .记
.记 .根据以上信息,可以得到函数
.根据以上信息,可以得到函数 的零点个数为 ( )
的零点个数为 ( )
| A.15 | B.10 |
| C.9 | D.8 |
已知函数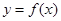 的周期为2,当
的周期为2,当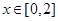 时,
时, ,如果
,如果
 ,则函数
,则函数 的所有零点之和为( )
的所有零点之和为( )
| A.2 | B.4 | C.6 | D.8 |
 的函数
的函数 ,若存在非零实数
,若存在非零实数 ,使函数
,使函数 和
和 上均有零点,则称
上均有零点,则称



 其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:①若P∩M=
其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:①若P∩M=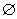 ,则f(P)∩f(M)=
,则f(P)∩f(M)=