题目内容
函数 的单调递减区间是( )
的单调递减区间是( )
A. | B. | C. | D. |
B
解析试题分析:因为由已知可知函数 的定义域为
的定义域为 ,而外层函数
,而外层函数 是定义域内的减函数,要求解函数的单调减区间,只要求解内层的增区间即可,而对于内层的
是定义域内的减函数,要求解函数的单调减区间,只要求解内层的增区间即可,而对于内层的 ,在
,在 上递增,故利用复合函数的同增异减,得到答案为B.
上递增,故利用复合函数的同增异减,得到答案为B.
考点:本试题主要是考查了函数单调性的判定,以及复合函数的同增异减的判定法则的应用。
点评:解决该试题的易错点就是对于定义域的忽略求解,以及复合函数的判定法则的熟练程度,是考查了分析和解决问题的能力。

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
已知函数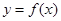 的周期为2,当
的周期为2,当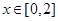 时,
时, ,如果
,如果
 ,则函数
,则函数 的所有零点之和为( )
的所有零点之和为( )
| A.2 | B.4 | C.6 | D.8 |
函数 和
和 的递增区间依次是( )
的递增区间依次是( )
A.(-∞,0 ,(-∞,1 ,(-∞,1 | B.(-∞,0 ,[1,+∞ ,[1,+∞ |
C.[0,+∞ ,(-∞,1 ,(-∞,1 | D.[0,+∞),[1,+∞) |
已知函数 的零点分别为
的零点分别为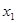 ,
, ,则( )
,则( )
A. | B. |
C. | D. |
定义域是一切实数的函数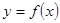 ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数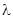 (
(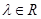 )使得
)使得  对任意实数
对任意实数 都成立,则称
都成立,则称 是一个“
是一个“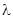 —伴随函数”.有下列关于“
—伴随函数”.有下列关于“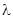 —伴随函数”的结论:
—伴随函数”的结论:
① 是常数函数中唯一一个“
是常数函数中唯一一个“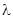 —伴随函数”;
—伴随函数”;
②“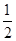 —伴随函数”至少有一个零点;
—伴随函数”至少有一个零点;
③ 是一个“
是一个“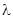 —伴随函数”;
—伴随函数”;
其中正确结论的个数是 ( )
| A.1个; | B.2个; | C.3个; | D.0个; |
定义域是一切实数的函数 ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数 (
( )
)
使得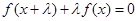 对任意实数
对任意实数 都成立,则称
都成立,则称 是一个“
是一个“ —伴随函数”. 有
—伴随函数”. 有
下列关于“ —伴随函数”的结论:
—伴随函数”的结论:
① 是常数函数中唯一一个“
是常数函数中唯一一个“ —伴随函数”;
—伴随函数”;
②“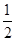 —伴随函数”至少有一个零点;
—伴随函数”至少有一个零点;
③ 是一个“
是一个“ —伴随函数”;
—伴随函数”;
其中正确结论的个数是 ( )
| A.1个; | B.2个; | C.3个; | D.0个; |
已知函数 ,若
,若 ,则
,则 等于 ( )
等于 ( )
A. | B. | C. | D. |
若奇函数 在
在 上为增函数,且有最小值0,则它在
上为增函数,且有最小值0,则它在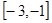 上( )
上( )
| A.是减函数,有最小值0 | B.是增函数,有最小值0 |
| C.是减函数,有最大值0 | D.是增函数,有最大值0 |
 其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:①若P∩M=
其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:①若P∩M=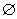 ,则f(P)∩f(M)=
,则f(P)∩f(M)=