题目内容
在四棱锥 中,底面
中,底面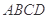 是正方形,侧面
是正方形,侧面 是正三角形,平面
是正三角形,平面 底面
底面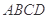 .
.

(Ⅰ)如果 为线段VC的中点,求证:
为线段VC的中点,求证: 平面
平面 ;
;
(Ⅱ)如果正方形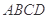 的边长为2, 求三棱锥
的边长为2, 求三棱锥 的体积
的体积
 中,底面
中,底面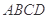 是正方形,侧面
是正方形,侧面 是正三角形,平面
是正三角形,平面 底面
底面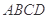 .
.
(Ⅰ)如果
 为线段VC的中点,求证:
为线段VC的中点,求证: 平面
平面 ;
;(Ⅱ)如果正方形
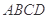 的边长为2, 求三棱锥
的边长为2, 求三棱锥 的体积
的体积(Ⅰ)见解析;(Ⅱ) .
.
 .
.试题分析:(Ⅰ)连结AC与BD交于点O, 连结OP,证明OP∥VA;(Ⅱ)在平面VAD内,过点V作VH⊥AD,证明VH⊥面
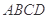 ,然后计算体积.
,然后计算体积.试题解析:(Ⅰ)连结AC与BD交于点O, 连结OP
因为ABCD是正方形,所以OA=OC,又因为PV=PC
所以OP∥VA,又因为
 面PBD,所以
面PBD,所以 平面
平面 --------6分
--------6分(Ⅱ)在平面VAD内,过点V作VH⊥AD,因为平面
 底面
底面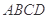 .所以VH⊥面
.所以VH⊥面
所以
 --------- 12分
--------- 12分

练习册系列答案
相关题目

 中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
, ,
, 分别是
分别是 的中点
的中点
 ∥平面
∥平面 ;
; ;
; 的体积.
的体积.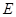 是以
是以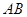 为直径的半圆上异于点
为直径的半圆上异于点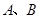 的点,矩形
的点,矩形 所在的平面垂直于该半圆所在平面,且
所在的平面垂直于该半圆所在平面,且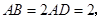
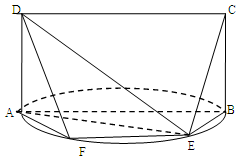
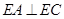 ;
;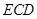 与半圆弧的另一个交点为
与半圆弧的另一个交点为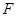 ,
,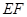 //
//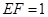 ,求三棱锥E-ADF的体积.
,求三棱锥E-ADF的体积. 中,
中,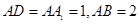 ,点E是AB的中点.
,点E是AB的中点.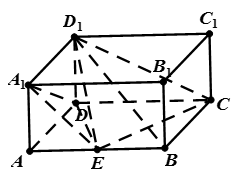
 的体积;
的体积;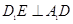 ;
; 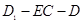 的正切值.
的正切值. 的所有顶点都在球
的所有顶点都在球 的球面上,
的球面上, 是边长为
是边长为 的正三角形,
的正三角形, 为球
为球 ,则此棱锥的体积为 .
,则此棱锥的体积为 . ,
, ,则四面体P-EFQ的体积( )
,则四面体P-EFQ的体积( )