题目内容
如图,已知在四棱锥P﹣ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,F,G分别是PD,PC,BC的中点.

(1)求证:平面EFG⊥平面PAD;
(2)若M是线段CD上一点,求三棱锥M﹣EFG的体积.

(1)求证:平面EFG⊥平面PAD;
(2)若M是线段CD上一点,求三棱锥M﹣EFG的体积.
(1)详见解析;(2)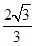 .
.
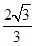 .
.试题分析:(1)要证明面面垂直,只需在一个平面内找到另一平面的一条垂线.由已知平面
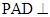 平面
平面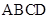 ,且
,且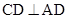 ,可证
,可证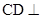 平面
平面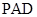 ,再根据
,再根据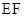 是中位线,可证
是中位线,可证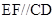 ,从而
,从而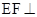 平面
平面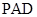 ,进而再证平面
,进而再证平面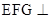 平面
平面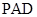 ,该题实质是先找到面
,该题实质是先找到面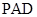 的一条垂线
的一条垂线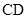 ,再将
,再将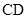 平移到面
平移到面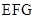 内;
内;(2)点
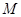 是线段
是线段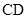 的动点,考虑到
的动点,考虑到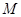 和
和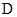 到面
到面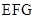 的距离相等,故
的距离相等,故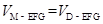 ,再结合第(1)问结果,取
,再结合第(1)问结果,取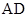 的中点
的中点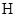 连接
连接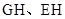 ,据面面垂直的性质,点
,据面面垂直的性质,点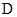 到
到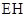 的距离就是三棱锥
的距离就是三棱锥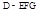 的高,再求
的高,再求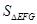 ,进而求体积.
,进而求体积.试题解析:(1)∵平面
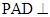 平面
平面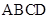 ,平面
,平面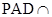 平面
平面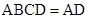 ,
,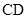
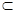 平面
平面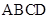 ,
,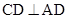 ,
,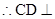 平面
平面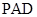 ,又
,又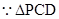 中,
中, 分别是
分别是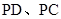 的中点,
的中点, ,可得
,可得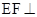 平面
平面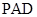 ,
,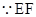
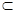 平面
平面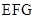 ,∴平面
,∴平面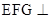 平面
平面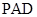 ;
;(2)
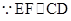 ,
,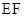
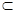 平面
平面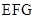 ,
,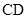
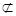 平面
平面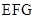 ,
,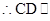 平面
平面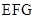 ,因此
,因此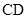 上的点
上的点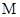 到平面
到平面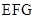 的距离等于点
的距离等于点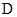 到平面
到平面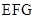 的距离,∴
的距离,∴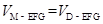 ,取
,取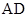 的中点
的中点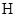 连接
连接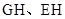 ,则
,则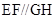 ,
,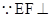 平面
平面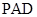 ,
,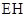
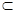 平面
平面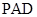 ,∴
,∴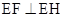 ,于是
,于是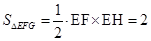 ,
,∵平面
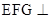 平面
平面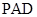 ,平面
,平面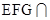 平面
平面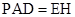 ,
,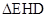 是正三角形,∴点
是正三角形,∴点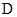 到平面
到平面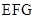 的距离等于正
的距离等于正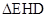 的高,即为
的高,即为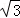 ,因此,三棱锥M﹣EFG的体积
,因此,三棱锥M﹣EFG的体积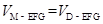 =
=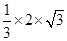 =
=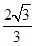 .
.
练习册系列答案
相关题目
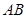 和AB1的中点,点F在BC上且满足BF∶FC=1∶3.
和AB1的中点,点F在BC上且满足BF∶FC=1∶3.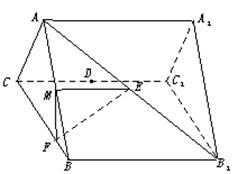
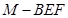 的体积.
的体积. 中,底面
中,底面 是边长为
是边长为 的菱形,
的菱形, ,
,  底面
底面 ,
, 为
为 的中点,
的中点, 为
为 的中点.
的中点.
 平面
平面 .
. 中,底面
中,底面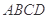 是正方形,侧面
是正方形,侧面 是正三角形,平面
是正三角形,平面 底面
底面
 为线段VC的中点,求证:
为线段VC的中点,求证: 平面
平面 ;
; 的体积
的体积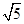 .
.
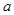 的三棱锥的四个顶点全部在同一个球面上,则该球的表面积为( )
的三棱锥的四个顶点全部在同一个球面上,则该球的表面积为( )



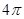
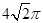
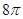
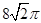





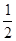 ,则其体积缩小到原来的
,则其体积缩小到原来的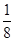 ;
;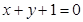 与圆
与圆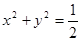 相切.
相切.