题目内容
9．已知抛物线x2=4y上的动点P在x轴上的射影为点M，点A（3，2），则|PA|+|PM|的最小值为$\sqrt{10}$-1．分析 先根据抛物线方程求得焦点和准线方程，可把问题转化为P到准线与P到A点距离之和最小，进而根据抛物线的定义可知抛物线中P到准线的距离等于P到焦点的距离，进而推断出P、A、F三点共线时|PF|+|PA|距离之和最小，利用两点间距离公式求得|FA|，则|PA|+|PM|可求．
解答 解：依题意可知，抛物线焦点为（0，1），准线方程为y=-1，
只需直接考虑P到准线与P到A点距离之和最小即可，
（因为x轴与准线间距离为定值1，不会影响讨论结果），
由于在抛物线中P到准线的距离等于P到焦点的距离，
此时问题进一步转化为|PF|+|PA|距离之和最小即可（F为曲线焦点），
显然当P、A、F三点共线时|PF|+|PA|距离之和最小，为|FA|，
由两点间距离公式得|FA|=$\sqrt{1+9}$=$\sqrt{10}$，
那么P到A的距离与P到x轴距离之和的最小值为|FA|-1=$\sqrt{10}$-1．
故答案为：$\sqrt{10}$-1．
点评 本题主要考查了抛物线的简单性质．考查了学生数形结合的思想和分析推理能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
19．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1与直线y=2x有公共点与y=3x没有公共点，则双曲线的离心率的取值范围为（ ）
| A． | （$\sqrt{5}$，$\sqrt{10}$] | B． | （1，$\sqrt{10}$] | C． | （1，$\sqrt{5}$] | D． | [$\sqrt{5}$，+∞） |
17．设复数z=1+i（i是虚数单位），则|$\frac{2}{z}$+z2|=（ ）
| A． | 1+i | B． | -1+i | C． | $\sqrt{2}$ | D． | 2 |
4．
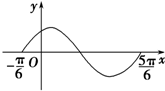如图是函数y=sin（ωx+φ）（ω＞0，0＜φ＜$\frac{π}{2}$）在区间[-$\frac{π}{6}$，$\frac{5π}{6}$]上的图象，将该图象向右平移m（m＞0）个单位后，所得图象关于直线x=$\frac{π}{4}$对称，则m的最小值为（ ）
如图是函数y=sin（ωx+φ）（ω＞0，0＜φ＜$\frac{π}{2}$）在区间[-$\frac{π}{6}$，$\frac{5π}{6}$]上的图象，将该图象向右平移m（m＞0）个单位后，所得图象关于直线x=$\frac{π}{4}$对称，则m的最小值为（ ）| A． | $\frac{π}{12}$ | B． | $\frac{π}{6}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{3}$ |
14．双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1的离心率为（ ）
| A． | $\frac{\sqrt{5}}{2}$ | B． | $\frac{3}{2}$ | C． | $\frac{9}{4}$ | D． | $\frac{5}{3}$ |
19．在△ABC中，角A，B，C的对边为a，b，c，b=8，c=8$\sqrt{3}$，S△ABC=16$\sqrt{3}$，则A等于（ ）
| A． | 30° | B． | 60° | C． | 30°或150° | D． | 60°或120° |