题目内容
18.已知实数x,y满足$\left\{\begin{array}{l}x+y+1≥0\\ 2x-y+2≥0\end{array}\right.$,若(-1,0)是使ax+y取得最大值的可行解,则实数a的取值范围是(-∞,-2].分析 作出不等式组对应的平面区域,根据目标函数z=ax+y在点(-1,0)有最优解,结合图形即可求出实数a的取值范围.
解答 解:可行域如图: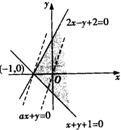
直线2x-y+2=0的斜率为2,
要使ax+y在(-1,0)处取得最大值,
则ax+y对应的直线的斜率k≥2,
所以-a≥2,即a≤-2.
故答案为:(-∞,-2].
点评 本题主要考查了简单的线性规划,以及利用几何意义求最值的方法反求参数的范围,属于基础题.

练习册系列答案
相关题目
6.定义:$|\begin{array}{l}{{a}_{1}}&{{a}_{2}}\\{{a}_{3}}&{{a}_{4}}\end{array}|$=a1a4-a2a3,若函数f(x)=$|\begin{array}{l}{\sqrt{3}}&{1}\\{cosx}&{sinx}\end{array}|$,将其图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( )
| A. | $\frac{π}{3}$ | B. | $\frac{2}{3}$π | C. | $\frac{π}{6}$ | D. | $\frac{5}{6}$π |
10.若复数z满足z(1+i)=4-2i(i为虚数单位),则|z|=( )
| A. | $\sqrt{10}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |