Question

【题目】已知椭圆C： + =1（a＞b＞0），短轴长2，两焦点分别为F1 ， F2 ， 过F1的直线交椭圆C于M，N两点，且△F2MN的周长为8．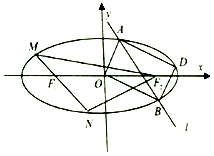

（1）求椭圆C的方程；
（2）直线l与椭圆C相交于A，B点，点D为椭圆C上一点，四边形AOBD为矩形，求直线l的方程．

Answer 1

【答案】
（1）

解：由题意可得：2b=2，4a=8，解得b=1，a=2．

∴椭圆C的方程为 +y2=1

（2）

解：由题意可设直线l的方程为：y=kx+m，A（x1，y1），B（x2，y2）．

联立 ，化为：（1+4k2）x2+8km+4m2﹣4=0，△＞0．

∴x1x2= ，x1+x2= ．

∵OA⊥OB，∴ =x1x2+y1y2=0，即x1x2+（kx1+m）（kx2+m）=0，化为：k2x1x2+km（x1+x2）+m2=0．

∴k2× +km× +m2=0．

化为：m2=4k2．

设线段AB的中点G（x0，y0），则x0= = ，y0= +m= ．

∴D ，代入椭圆方程可得： +4× =4，

化为：16k2m2+4m2=1+8k2+16k4，

把m2=4k2代入上述方程可得：3m4+2m2﹣1=0．

解得m= ，解得k= ．

∴直线l的方程为y= x

【解析】（1）由题意可得：2b=2，4a=8，解得b，a．可得椭圆C的方程．（2）由题意可设直线l的方程为：y=kx+m，A（x1 ， y1），B（x2 ， y2）．与椭圆方程联立化为：（1+4k2）x2+8km+4m2﹣4=0，△＞0．由OA⊥OB，可得 =x1x2+y1y2=0，即k2x1x2+km（x1+x2）+m2=0．利用根与系数的关系化为：m2=4k2 ． 设线段AB的中点G（x0 ， y0），则x0= ，y0 ． 可得D坐标代入椭圆方程解出即可得出．