题目内容
如图,椭圆E: =1(a>b>0)的左焦点为F1,右焦点为F2,离心率e=
=1(a>b>0)的左焦点为F1,右焦点为F2,离心率e= .过F1的直线交椭圆于A、B两点,且△ABF2的周长为8.
.过F1的直线交椭圆于A、B两点,且△ABF2的周长为8.

(1)求椭圆E的方程;
(2)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q.试探究:在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由.
 =1(a>b>0)的左焦点为F1,右焦点为F2,离心率e=
=1(a>b>0)的左焦点为F1,右焦点为F2,离心率e= .过F1的直线交椭圆于A、B两点,且△ABF2的周长为8.
.过F1的直线交椭圆于A、B两点,且△ABF2的周长为8.
(1)求椭圆E的方程;
(2)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q.试探究:在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由.
(1)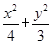 =1(2)存在定点M(1,0),
=1(2)存在定点M(1,0),
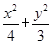 =1(2)存在定点M(1,0),
=1(2)存在定点M(1,0),学生错解:解:(1)略
(2)由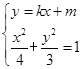 消去y得(4k2+3)x2+8kmx+4m2-12=0.
消去y得(4k2+3)x2+8kmx+4m2-12=0.
因为动直线l与椭圆E有且只有一个公共点P(x0,y0),所以m≠0且Δ=0,
即64k2m2-4(4k2+3)(4m2-12)=0,化简得4k2-m2+3=0.(*)
此时x0=-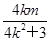 =-
=-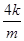 ,y0=kx0+m=
,y0=kx0+m=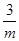 ,所以P
,所以P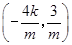 .
.
由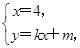 得Q(4,4k+m).
得Q(4,4k+m).
假设平面内存在定点M满足条件,由图形对称性知,点M必在x轴上.
设M(x1,0),则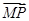 ·
·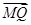 =0对满足(*)式的m,k恒成立.
=0对满足(*)式的m,k恒成立.
因为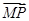 =
= ,
,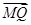 =(4-x1,4k+m),
=(4-x1,4k+m),
由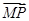 ·
·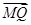 =0,得-
=0,得-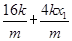 -4x1+
-4x1+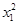 +
+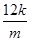 +3=0,
+3=0,
整理,得(4x1-4)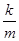 +
+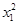 -4x1+3=0.(**),方程无解.
-4x1+3=0.(**),方程无解.
故不存在定点M,使得以PQ为直径的圆恒过点M.
审题引导:(1)建立方程组求解参数a,b,c;(2)恒成立问题的求解;(3)探索性问题的一般解题思路.
规范解答:解:(1)因为AB+AF2+BF2=8,
即AF1+F1B+AF2+BF2=8,(1分)
又AF1+AF2=BF1+BF2=2a,(2分)
所以4a=8,a=2.又因为e= ,即
,即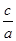 =
= ,所以c=1,(3分)
,所以c=1,(3分)
所以b= =
=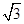 .故椭圆E的方程是
.故椭圆E的方程是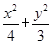 =1.(4分)
=1.(4分)
(2)由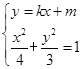 消去y得(4k2+3)x2+8kmx+4m2-12=0.(5分)
消去y得(4k2+3)x2+8kmx+4m2-12=0.(5分)
因为动直线l与椭圆E有且只有一个公共点P(x0,y0),所以m≠0且Δ=0,(6分)
即64k2m2-4(4k2+3)(4m2-12)=0,化简得4k2-m2+3=0.(*)(7分)
此时x0=-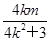 =-
=-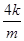 ,y0=kx0+m=
,y0=kx0+m=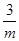 ,所以P
,所以P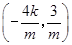 .(8分)
.(8分)
由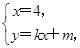 得Q(4,4k+m).(9分)
得Q(4,4k+m).(9分)
假设平面内存在定点M满足条件,由图形对称性知,点M必在x轴上.(10分)
设M(x1,0),则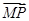 ·
·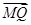 =0对满足(*)式的m,k恒成立.
=0对满足(*)式的m,k恒成立.
因为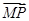 =
= ,
,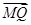 =(4-x1,4k+m),
=(4-x1,4k+m),
由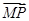 ·
·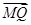 =0,得-
=0,得-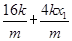 -4x1+
-4x1+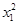 +
+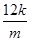 +3=0,
+3=0,
整理,得(4x1-4)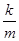 +
+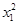 -4x1+3=0.(**)(12分)
-4x1+3=0.(**)(12分)
由于(**)式对满足(*)式的m,k恒成立,所以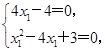 解得x1=1.(13分)
解得x1=1.(13分)
故存在定点M(1,0),使得以PQ为直径的圆恒过点M.(14分)
错因分析:本题易错之处是忽视定义的应用;在处理第(2)问时,不清楚圆的对称性,从而不能判断出点M必在x轴上.同时不会利用恒成立求解.
(2)由
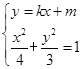 消去y得(4k2+3)x2+8kmx+4m2-12=0.
消去y得(4k2+3)x2+8kmx+4m2-12=0.因为动直线l与椭圆E有且只有一个公共点P(x0,y0),所以m≠0且Δ=0,
即64k2m2-4(4k2+3)(4m2-12)=0,化简得4k2-m2+3=0.(*)
此时x0=-
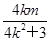 =-
=-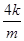 ,y0=kx0+m=
,y0=kx0+m=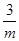 ,所以P
,所以P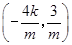 .
.由
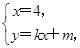 得Q(4,4k+m).
得Q(4,4k+m).假设平面内存在定点M满足条件,由图形对称性知,点M必在x轴上.
设M(x1,0),则
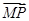 ·
·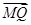 =0对满足(*)式的m,k恒成立.
=0对满足(*)式的m,k恒成立.因为
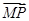 =
= ,
,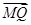 =(4-x1,4k+m),
=(4-x1,4k+m),由
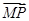 ·
·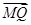 =0,得-
=0,得-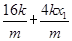 -4x1+
-4x1+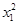 +
+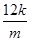 +3=0,
+3=0,整理,得(4x1-4)
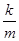 +
+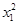 -4x1+3=0.(**),方程无解.
-4x1+3=0.(**),方程无解.故不存在定点M,使得以PQ为直径的圆恒过点M.
审题引导:(1)建立方程组求解参数a,b,c;(2)恒成立问题的求解;(3)探索性问题的一般解题思路.
规范解答:解:(1)因为AB+AF2+BF2=8,
即AF1+F1B+AF2+BF2=8,(1分)
又AF1+AF2=BF1+BF2=2a,(2分)
所以4a=8,a=2.又因为e=
 ,即
,即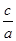 =
= ,所以c=1,(3分)
,所以c=1,(3分)所以b=
 =
=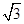 .故椭圆E的方程是
.故椭圆E的方程是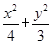 =1.(4分)
=1.(4分)(2)由
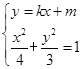 消去y得(4k2+3)x2+8kmx+4m2-12=0.(5分)
消去y得(4k2+3)x2+8kmx+4m2-12=0.(5分)因为动直线l与椭圆E有且只有一个公共点P(x0,y0),所以m≠0且Δ=0,(6分)
即64k2m2-4(4k2+3)(4m2-12)=0,化简得4k2-m2+3=0.(*)(7分)
此时x0=-
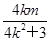 =-
=-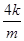 ,y0=kx0+m=
,y0=kx0+m=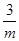 ,所以P
,所以P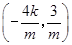 .(8分)
.(8分)由
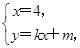 得Q(4,4k+m).(9分)
得Q(4,4k+m).(9分)假设平面内存在定点M满足条件,由图形对称性知,点M必在x轴上.(10分)
设M(x1,0),则
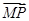 ·
·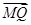 =0对满足(*)式的m,k恒成立.
=0对满足(*)式的m,k恒成立.因为
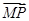 =
= ,
,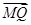 =(4-x1,4k+m),
=(4-x1,4k+m),由
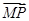 ·
·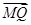 =0,得-
=0,得-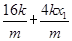 -4x1+
-4x1+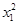 +
+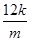 +3=0,
+3=0,整理,得(4x1-4)
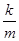 +
+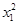 -4x1+3=0.(**)(12分)
-4x1+3=0.(**)(12分)由于(**)式对满足(*)式的m,k恒成立,所以
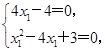 解得x1=1.(13分)
解得x1=1.(13分)故存在定点M(1,0),使得以PQ为直径的圆恒过点M.(14分)
错因分析:本题易错之处是忽视定义的应用;在处理第(2)问时,不清楚圆的对称性,从而不能判断出点M必在x轴上.同时不会利用恒成立求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是平面直角坐标系上的一个动点,点
是平面直角坐标系上的一个动点,点 到直线
到直线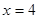 的距离等于点
的距离等于点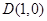 的距离的2倍.记动点
的距离的2倍.记动点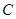 .
.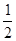 的直线
的直线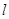 与曲线
与曲线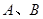 两个不同点,若直线
两个不同点,若直线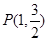 ,设直线
,设直线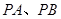 的斜率分别为
的斜率分别为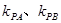 ,求
,求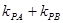 的数值;
的数值; ,与以动点
,与以动点 为半径的圆相内切?若存在,求出这个定圆的方程;若不存在,说明理由.
为半径的圆相内切?若存在,求出这个定圆的方程;若不存在,说明理由. (
( )的短轴长为2,离心率为
)的短轴长为2,离心率为
 的直线与椭圆C相交于两点G、H,设P为椭圆C上一点,且满足
的直线与椭圆C相交于两点G、H,设P为椭圆C上一点,且满足 (
( 为坐标原点),当
为坐标原点),当 时,求实数
时,求实数 的取值范围?
的取值范围? ,椭圆
,椭圆 以
以 的长轴为短轴,且与
的长轴为短轴,且与 为坐标原点,点
为坐标原点,点 、
、 分别在椭圆
分别在椭圆 ,求直线
,求直线 的方程.
的方程.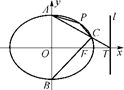
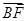 =3
=3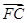 ,四边形APCB的面积最大值为
,四边形APCB的面积最大值为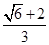 ,求此时椭圆的方程和P点坐标.
,求此时椭圆的方程和P点坐标. +y2=1,A、B是四条直线x=±2,y=±1所围成的矩形的两个顶点.
+y2=1,A、B是四条直线x=±2,y=±1所围成的矩形的两个顶点.
 =m
=m +n
+n ,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程;
,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程; 的焦距为2,且过点
的焦距为2,且过点 .
. ,
, ,过点
,过点 与椭圆C交于
与椭圆C交于 两点.
两点. 时,求
时,求 的长;
的长; 的内切圆的面积的最大值,并求出当
的内切圆的面积的最大值,并求出当 =1的左、右两个焦点,若椭圆上满足PF1⊥PF2的点P有且只有两个,则离心率e的值为( )
=1的左、右两个焦点,若椭圆上满足PF1⊥PF2的点P有且只有两个,则离心率e的值为( )


 =1的离心率为________.
=1的离心率为________.