题目内容
(本小题满分12分)
(如右图) 在正方体ABCD-A1B1C1D1中,
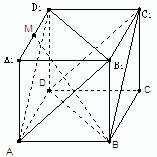
(1)证明:平面AB1D1∥平面BDC1
(2)设M为A1D1的中点,求直线BM与平面BB1D1D所成角的正弦值.
(如右图) 在正方体ABCD-A1B1C1D1中,

(1)证明:平面AB1D1∥平面BDC1
(2)设M为A1D1的中点,求直线BM与平面BB1D1D所成角的正弦值.
(1)(略) (2)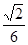
对于第一问先在平面AB1D1找两条相交直线AB1,AD1分别平行于平面BDC1
由面面平行的判定定理就可以证明平面AB1D1∥平面BDC1;第二问过M点作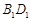 的垂线交
的垂线交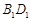 于点E,连接BE,可证∠MBE为线BM与平面BB1D1D所成角,然后解三角形求出角的正弦值。
于点E,连接BE,可证∠MBE为线BM与平面BB1D1D所成角,然后解三角形求出角的正弦值。
由面面平行的判定定理就可以证明平面AB1D1∥平面BDC1;第二问过M点作
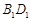 的垂线交
的垂线交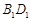 于点E,连接BE,可证∠MBE为线BM与平面BB1D1D所成角,然后解三角形求出角的正弦值。
于点E,连接BE,可证∠MBE为线BM与平面BB1D1D所成角,然后解三角形求出角的正弦值。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
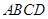 所在平面与三角形
所在平面与三角形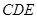 所在平面相交于
所在平面相交于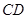 ,
,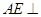 平面
平面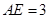 ,
,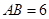
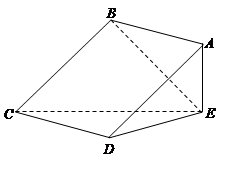
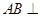 平面
平面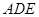 ;
;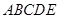 的体积.
的体积.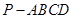 中,
中,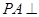 平面
平面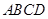 ,四边形
,四边形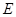 ,
,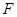 分别是
分别是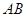 ,
,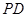 的中点.若
的中点.若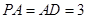 ,
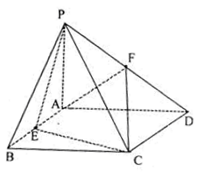
,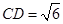 。
。
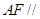 平面
平面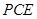 ;
;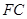 平面
平面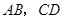 的长度分别等于
的长度分别等于 分别为
分别为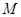 ;②弦
;②弦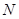 ;
;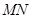 的最大值为5; ④
的最大值为5; ④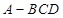 中,侧棱
中,侧棱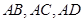 两两垂直,
两两垂直,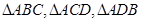 的
的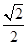 、
、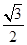 、
、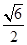 .则三棱锥
.则三棱锥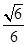
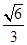
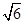
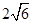
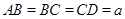 ,
,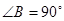 ,
,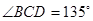 ,沿对角线
,沿对角线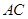 将
将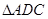 折起,使面
折起,使面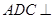 面
面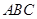 ,
,
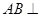 面
面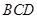 ;
;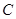 到面
到面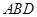 的距离.
的距离.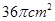 ,则这个球的体积为
,则这个球的体积为 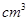 。
。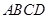 的外接球的球心为
的外接球的球心为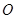 ,
,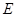 是
是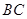 的中点,则直线
的中点,则直线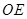 和平面
和平面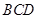 所成角的正切值为 。
所成角的正切值为 。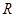 ,若甲地位于北纬
,若甲地位于北纬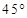 东经
东经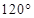 ,乙地位于南纬
,乙地位于南纬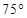 东经
东经


