题目内容
3.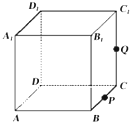 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S. ①当0<CQ<$\frac{1}{2}$时,S为四边形
②截面在底面上投影面积恒为定值$\frac{3}{4}$
③存在某个位置,使得截面S与平面A1BD垂直
④当CQ=$\frac{3}{4}$时,S与C1D1的交点R满足C1R=$\frac{1}{3}$
其中正确命题的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 对选项逐个进行检验即可,对于①:得到0<DT<1,可以容易得到S为四边形;对于②则找其投影即可;对于③,则需要找线面垂直关系即可;对于④,则需补图完成.
解答 解:设截面与DD1相交于T,则AT∥PQ,且AT=2PQ⇒DT=2CQ.
对于①,当0<CQ<$\frac{1}{2}$时,则0<DT<1,所以截面S为四边形,且S为梯形,故①正确;
对于②,当CQ>$\frac{1}{2}$时,投影面积不为$\frac{3}{4}$,故②不正确;
对于③,存在某个位置,使得截面S与平面A1BD垂直,故③正确;
对于④,右补充一个正方体后,得到S与C1D1的交点R满足C1R=$\frac{1}{3}$,故④正确;
故选:C.
点评 本题重点考查了空间几何体的结构特征、空间中点线面的位置关系等知识,对于中点问题的处理思路是:无中点,取中点,相连得到中位线.属于中档题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
2.若在△ABC中,2cosBsinA=sinC,则△ABC的形状一定是( )
| A. | 等腰直角三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 等边三角形 |
8.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和圆O:x2+y2=b2,若C上存在点M,过点M引圆O的两条切线,切点分别为E,F,使得△MEF为正三角形,则椭圆C的离心率的取值范围是( )
| A. | [$\frac{1}{2}$,1) | B. | [$\frac{\sqrt{2}}{2}$,1) | C. | [$\frac{\sqrt{3}}{2}$,1) | D. | (1,$\frac{3}{2}$] |
15.已知函数f(x)=mlnx-$\frac{{x}^{2}}{2}$,f(x)的导函数为f′(x),对?x∈(0,1),有f′(x)•f′(1-x)≤1恒成立,则实数m的取值范围为( )
| A. | (0,$\frac{3}{4}$] | B. | [0,$\frac{3}{4}$] | C. | [0,1) | D. | [0,1] |
 如图,在底面为菱形的四棱锥P-ABCD中,∠BAD=120°,PA⊥底面ABCD,且PA=AB=6,E是棱PD的三等分点(PE>ED),F是棱PC的中点,底面对角线AC与BD相交于点O.
如图,在底面为菱形的四棱锥P-ABCD中,∠BAD=120°,PA⊥底面ABCD,且PA=AB=6,E是棱PD的三等分点(PE>ED),F是棱PC的中点,底面对角线AC与BD相交于点O.