题目内容
14.设定义在(0,+∞)上的函数f(x)=$\left\{\begin{array}{l}2x,x≤0\\{x^2}-2x-\frac{3}{2},x>0\end{array}$,g(x)=f(x)+a,则当实数a满足2<a<$\frac{5}{2}$时,函数y=g(x)的零点个数为( )| A. | 0 | B. | 2 | C. | 3 |
分析 画出分段函数的图象,转化函数的零点为方程的根,利用函数的图象推出结果即可.
解答  解:函数y=g(x)的零点个数,就是方程g(x)=f(x)+a=0方程根的个数,即f(x)=-a根的个数,也就是函数f(x)与y=-a图象交点的个数,
解:函数y=g(x)的零点个数,就是方程g(x)=f(x)+a=0方程根的个数,即f(x)=-a根的个数,也就是函数f(x)与y=-a图象交点的个数,
函数f(x)=$\left\{\begin{array}{l}2x,x≤0\\{x^2}-2x-\frac{3}{2},x>0\end{array}$与y=-a,2<a<$\frac{5}{2}$的图象如图:
2<a<$\frac{5}{2}$可得-2>-a>-$\frac{5}{2}$.
由图象可知,两个函数的交点有3个.
故选:C.
点评 本题考查函数的零点与方程的根的关系,零点的个数的判断,考查转化思想以及数形结合的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
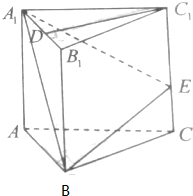 如图,在直三棱柱ABC-A1B1C1中,D、E分别是棱A1B1、CC1的点,且DC1⊥A1B1,A1D=$\frac{2}{3}$A1B1,CE=$\frac{1}{3}$CC1,求证:
如图,在直三棱柱ABC-A1B1C1中,D、E分别是棱A1B1、CC1的点,且DC1⊥A1B1,A1D=$\frac{2}{3}$A1B1,CE=$\frac{1}{3}$CC1,求证: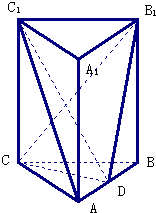 三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为AB边中点,且CC1=2AB.
三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为AB边中点,且CC1=2AB. 已知四棱锥P-ABCD中,底面ABCD是菱形,M是PC的中点,∠PDC=90°,∠PDA=90°,∠DAB=60°
已知四棱锥P-ABCD中,底面ABCD是菱形,M是PC的中点,∠PDC=90°,∠PDA=90°,∠DAB=60° 如图,在直三棱柱ABC-A1B1C1中,D、E分别为CC1、AD的中点,F为BB1上的点,且B1F=3BF.
如图,在直三棱柱ABC-A1B1C1中,D、E分别为CC1、AD的中点,F为BB1上的点,且B1F=3BF. 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.