题目内容
11. 如图,在底面为菱形的四棱锥P-ABCD中,∠BAD=120°,PA⊥底面ABCD,且PA=AB=6,E是棱PD的三等分点(PE>ED),F是棱PC的中点,底面对角线AC与BD相交于点O.
如图,在底面为菱形的四棱锥P-ABCD中,∠BAD=120°,PA⊥底面ABCD,且PA=AB=6,E是棱PD的三等分点(PE>ED),F是棱PC的中点,底面对角线AC与BD相交于点O.(Ⅰ)求证:BD⊥PC;
(Ⅱ)求三棱锥A-CEF的体积.
分析 (I)由PA⊥底面ABCD,可得PA⊥BD,由菱形ABCD可得BD⊥AC,即可证明BD⊥平面PAC;
(II)设点E到平面PAC的距离为d,由E是棱PD的三等分点(PE>ED),BD⊥平面PAC,可得d=$\frac{2}{3}OD$,利用三棱锥A-CEF的体积V=VE-AFC=$\frac{1}{3}×d×{S}_{△AFC}$,即可得出.
解答 (I)证明:∵PA⊥底面ABCD,∴PA⊥BD,
由菱形ABCD可得BD⊥AC,PA∩AC=A.
∴BD⊥平面PAC,
∴BD⊥PC;
(II)解:菱形ABCD中,∠BAD=120°,AB=6.
则OA=3,OD=$3\sqrt{3}$.
设点E到平面PAC的距离为d,
∵E是棱PD的三等分点(PE>ED),BD⊥平面PAC,
∴d=$\frac{2}{3}OD$=2$\sqrt{3}$,
∵PA⊥底面ABCD,
∴PA⊥AC.
∴S△PAC=$\frac{1}{2}$×62=18.
∴S△AFC=$\frac{1}{2}{S}_{△PAC}$=9.
∴三棱锥A-CEF的体积V=VE-AFC=$\frac{1}{3}×d×{S}_{△AFC}$=$\frac{1}{3}×2\sqrt{3}×9$=6$\sqrt{3}$.
点评 本题考查了线面垂直的判定与性质定理、三棱锥的体积计算公式、菱形的性质、等边三角形与直角三角形的边角关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 如图,在直三棱柱ABC-A1B1C1中,D、E分别是棱A1B1、CC1的点,且DC1⊥A1B1,A1D=$\frac{2}{3}$A1B1,CE=$\frac{1}{3}$CC1,求证:
如图,在直三棱柱ABC-A1B1C1中,D、E分别是棱A1B1、CC1的点,且DC1⊥A1B1,A1D=$\frac{2}{3}$A1B1,CE=$\frac{1}{3}$CC1,求证: 已知四棱锥P-ABCD中,底面ABCD是菱形,M是PC的中点,∠PDC=90°,∠PDA=90°,∠DAB=60°
已知四棱锥P-ABCD中,底面ABCD是菱形,M是PC的中点,∠PDC=90°,∠PDA=90°,∠DAB=60° 如图,在直三棱柱ABC-A1B1C1中,D、E分别为CC1、AD的中点,F为BB1上的点,且B1F=3BF.
如图,在直三棱柱ABC-A1B1C1中,D、E分别为CC1、AD的中点,F为BB1上的点,且B1F=3BF.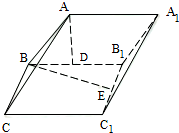
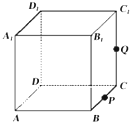 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.  如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=45°,PD⊥平面ABCD,PD=AD=1,点E为AB上一点,且$\frac{AE}{AB}$=k,点F为PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=45°,PD⊥平面ABCD,PD=AD=1,点E为AB上一点,且$\frac{AE}{AB}$=k,点F为PD中点.