题目内容
15.已知函数f(x)=mlnx-$\frac{{x}^{2}}{2}$,f(x)的导函数为f′(x),对?x∈(0,1),有f′(x)•f′(1-x)≤1恒成立,则实数m的取值范围为( )| A. | (0,$\frac{3}{4}$] | B. | [0,$\frac{3}{4}$] | C. | [0,1) | D. | [0,1] |
分析 由函数f(x)=mlnx-$\frac{{x}^{2}}{2}$,可得f′(x)=$\frac{m}{x}$-x.由于对?x∈(0,1),有f′(x)•f′(1-x)≤1恒成立,即$(\frac{m}{x}-x)[\frac{m}{1-x}-(1-x)]$≤1,化为[m-(x2-x+1)][m-(x2-x)]≤0,解出并利用二次函数的单调性即可得出.
解答 解:由函数f(x)=mlnx-$\frac{{x}^{2}}{2}$,
可得f′(x)=$\frac{m}{x}$-x,
∵对?x∈(0,1),有f′(x)•f′(1-x)≤1恒成立,
∴$(\frac{m}{x}-x)[\frac{m}{1-x}-(1-x)]$≤1,
化为[m-(x2-x+1)][m-(x2-x)]≤0,
当m≠0时,解得x2-x≤m≤x2-x+1,
∵x2-x=x(x-1)<0,x2-x+1=$(x-\frac{1}{2})^{2}+\frac{3}{4}$$≥\frac{3}{4}$.
∴$0<m≤\frac{3}{4}$.
当m=0时,有f′(x)•f′(1-x)=x(1-x)≤$(\frac{x+1-x}{2})^{2}$=$\frac{1}{4}$<1恒成立.
综上可得:实数m的取值范围为$[0,\frac{3}{4}]$.
故选:B.
点评 本题考查了导数的运算法则、恒成立问题等价转化方法、一元二次不等式的解法,考查了分析问题与解决问题的能力、计算能力,属于难题.

练习册系列答案
相关题目
 如图,在直三棱柱ABC-A1B1C1中,D、E分别为CC1、AD的中点,F为BB1上的点,且B1F=3BF.
如图,在直三棱柱ABC-A1B1C1中,D、E分别为CC1、AD的中点,F为BB1上的点,且B1F=3BF.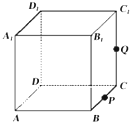 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.  如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=45°,PD⊥平面ABCD,PD=AD=1,点E为AB上一点,且$\frac{AE}{AB}$=k,点F为PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=45°,PD⊥平面ABCD,PD=AD=1,点E为AB上一点,且$\frac{AE}{AB}$=k,点F为PD中点.