题目内容
2．若在△ABC中，2cosBsinA=sinC，则△ABC的形状一定是（ ）| A． | 等腰直角三角形 | B． | 直角三角形 | C． | 等腰三角形 | D． | 等边三角形 |
分析 由题意和和差角公式易得sin（A-B）=0，进而可得A=B，可判△ABC为等腰三角形．
解答 解：∵在△ABC中2cosBsinA=sinC，
∴2cosBsinA=sinC=sin（A+B），
∴2cosBsinA=sinAcosB+cosAsinB，
∴sinAcosB-cosAsinB=0，
∴sin（A-B）=0，
∴A-B=0，即A=B，
∴△ABC为等腰三角形，
故选：C．
点评 本题考查三角形性质的判断，涉及和差角公式的应用，属基础题．
练习册系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
如图所示，设E，F，E1，F1分别是长方体ABCD-A1B1C1D1的棱AB，CD，A1B1，C1D1的中点，则平面EFD1A1与平面BCF1E1的位置关系是（ ）
如图，在直三棱柱ABC-A1B1C1中，D、E分别是棱A1B1、CC1的点，且DC1⊥A1B1，A1D=$\frac{2}{3}$A1B1，CE=$\frac{1}{3}$CC1，求证：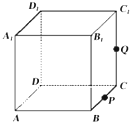
如图，正方体ABCD-A1B1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的动点，过点A，P，Q的平面截该正方体所得的截面记为S．