题目内容
18.已知函数f(x)=ex-m-x,其中m为常数.(1)若对任意x∈R有f(x)≥0成立,求m的取值范围;
(2)当m>1时,判断f(x)在[0,2m]上零点的个数,并说明理由.
分析 (1)求出原函数的导函数,得到导函数的零点,求出函数的单调区间,得到函数的最小值,由最小值大于等于0求得m的取值范围;
(2)当m>1时,由f(0)•f(m)<0,得到f(x)在(0,m)上有一个零点.再由导数求得f(2m)>0.
得到f(m)•f(2m)<0,得f(x)在(m,2m)上有一个零点.故可得f(x)在[0,2m]上有两个零点.
解答 解:(1)∵f(x)=ex-m-x,∴f′(x)=ex-m-1,
令f′(x)=0,得x=m.
故当x∈(-∞,m)时,ex-m<1,f′(x)<0,f(x)单调递减;
当x∈(m,+∞)时,ex-m>1,f′(x)>0,f(x)单调递增;
故当x=m时,f(m)为极小值,也是最小值.
令f(m)=1-m≥0,得m≤1,
即对任意x∈R,f(x)≥0恒成立时,m的取值范围是(-∞,1];
(2)由(1)知f(x)在[0,2m]上至多有两个零点,
当m>1时,f(m)=1-m<0.
∵f(0)=e-m>0,f(0)•f(m)<0,
∴f(x)在(0,m)上有一个零点.
又f(2m)=em-2m,令g(m)=em-2m,
∵当m>1时,g′(m)=em-2>0,
∴g(m)在(1,+∞)上单调递增.
∴g(m)>g(1)=e-2>0,即f(2m)>0.
∴f(m)•f(2m)<0,
∴f(x)在(m,2m)上有一个零点.
故f(x)在[0,2m]上有两个零点.
点评 本题考查了利用导数研究函数的单调性,考查了函数零点的判断方法,正确分类是解答(2)的关键,是中档题.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
8.在等腰梯形ABCD中,AB∥CD,且|AB|=2,|AD|=1,|CD|=2x其中x∈(0,1),以A,B为焦点且过点D的双曲线的离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,若对任意x∈(0,1)不等式t<e1+e2恒成立,则t的最大值为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{2}$ |
 三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为AB边中点,且CC1=2AB.
三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为AB边中点,且CC1=2AB. 如图,在直三棱柱ABC-A1B1C1中,D、E分别为CC1、AD的中点,F为BB1上的点,且B1F=3BF.
如图,在直三棱柱ABC-A1B1C1中,D、E分别为CC1、AD的中点,F为BB1上的点,且B1F=3BF.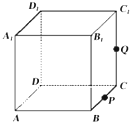 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S. 