题目内容
12.直线l方程为(2+m)x+(1-2m)y+4-3m=0(1)求证:无论m取何值,l过定点;
(2)设此定点为P,过P点作直线分别与两坐标轴交于A点和B点,若P为线段AB的中点,求l的方程.
分析 (1)方程变形为(x-2y-3)m+(2x+y+4)=0,即可得出无论m取何值,l过定点;
(2)求出A,B的坐标,可得l的方程.
解答 (1)证明:因为l的方程为(2+m)x+(1-2m)y+4-3m=0,
所以2x+mx+y-2my+4-3m=0,
所以(x-2y-3)m+(2x+y+4)=0,
所以$\left\{\begin{array}{l}{x-2y-3=0}\\{2x+y+4=0}\end{array}\right.$,
所以x=-1,y=-2,
所以直线过定点(-1,-2);
(2)解:P(-1,-2),
因为过P点作直线分别与两坐标轴交于A点和B点,P为线段AB的中点,
所以A(-2,0),B(0,-4),
所以l的方程为$\frac{x}{-2}+\frac{y}{-4}$=1.
点评 本题考查直线过定点,考查直线方程,考查学生的计算能力,比较基础.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
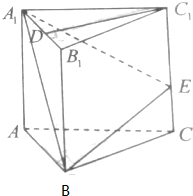 如图,在直三棱柱ABC-A1B1C1中,D、E分别是棱A1B1、CC1的点,且DC1⊥A1B1,A1D=$\frac{2}{3}$A1B1,CE=$\frac{1}{3}$CC1,求证:
如图,在直三棱柱ABC-A1B1C1中,D、E分别是棱A1B1、CC1的点,且DC1⊥A1B1,A1D=$\frac{2}{3}$A1B1,CE=$\frac{1}{3}$CC1,求证: 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.  如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=45°,PD⊥平面ABCD,PD=AD=1,点E为AB上一点,且$\frac{AE}{AB}$=k,点F为PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=45°,PD⊥平面ABCD,PD=AD=1,点E为AB上一点,且$\frac{AE}{AB}$=k,点F为PD中点.