题目内容
【题目】盒内有大小相同的9个球，其中2个红色球，3个白色球，4个黑色球. 规定取出1个红色球得1分，取出1个白色球得0分，取出1个黑色球得－1分 . 现从盒内任取3个球
（Ⅰ）求取出的3个球中至少有一个红球的概率；
（Ⅱ）求取出的3个球得分之和恰为1分的概率；
（Ⅲ）设
为取出的3个球中白色球的个数，求
的分布列.
【答案】解：（1）取出的3个球颜色互不相同的概率
，……………4分
（2）取出的3个球得分之和恰好为1分的概率
…8分
（3）ξ的分布列为：
0 1 2 3
P
数学期望
…………………12分
【解析】试题 （1）从9个球中取出3个球的所有可能情况有
种 . （1）从9个球中取出3个球颜色互不相同的所有可能情况有
,根据古典概型的概率公式可求其概率. （2） 取出的3个球得分之和恰好为1分的情况有:1个红球2个白球;2个红球1个黑球.对应的种数有
.根据古典概型的概率公式可求其概率. （3）
的可能取值有0,1,2,3.白色求共3个,非白色球共6个.则取出的白色球的个数
,则取出的3个球中含
个白色球对应的所有情况种数有
,根据古典概型的概率公式可求
.
试题解析：解：（1）取出的3个球颜色互不相同的概率
， 4分
（2）取出的3个球得分之和恰好为1分的概率8分
（3）ξ的分布列为：
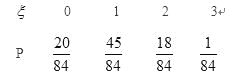
数学期望
12分
练习册系列答案
相关题目
【题目】某市环保部门为了让全市居民认识到冬天烧煤取暖对空气
数值的影响，进而唤醒全市人民的环保节能意识。对该市取暖季烧煤天数
与空气数值不合格的天数
进行统计分析，得出下表数据：
| 9 | 8 | 7 | 5 | 4 |
| 7 | 6 | 5 | 3 | 2 |
（1）以统计数据为依据，求出关于的线性回归方程
；
（2）根据（1）求出的线性回归方程，预测该市烧煤取暖的天数为20时空气数值不合格的天数．
参考公式：
，
．
