题目内容
(本小题满分14分)设函数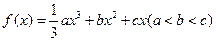 ,其图象对应的曲线设为G.(Ⅰ)设
,其图象对应的曲线设为G.(Ⅰ)设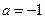 、
、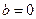 、
、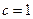 ,
,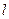 为经过点(2,2)的曲线G的切线,求
为经过点(2,2)的曲线G的切线,求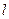 的方程;
的方程;
(Ⅱ)已知曲线G在点A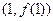 、B
、B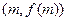 处的切线的斜率分别为0、
处的切线的斜率分别为0、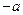 ,求证:
,求证: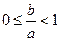 ;
;
(Ⅲ)在(Ⅱ)的条件下,当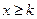 时,
时,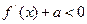 恒成立,求常数
恒成立,求常数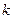 的最小值.
的最小值.
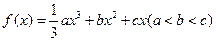 ,其图象对应的曲线设为G.(Ⅰ)设
,其图象对应的曲线设为G.(Ⅰ)设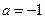 、
、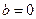 、
、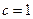 ,
,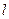 为经过点(2,2)的曲线G的切线,求
为经过点(2,2)的曲线G的切线,求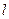 的方程;
的方程;(Ⅱ)已知曲线G在点A
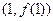 、B
、B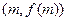 处的切线的斜率分别为0、
处的切线的斜率分别为0、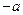 ,求证:
,求证: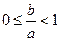 ;
;(Ⅲ)在(Ⅱ)的条件下,当
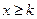 时,
时,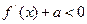 恒成立,求常数
恒成立,求常数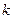 的最小值.
的最小值.(Ⅰ)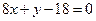 (Ⅱ)略(Ⅲ)
(Ⅱ)略(Ⅲ)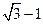
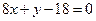 (Ⅱ)略(Ⅲ)
(Ⅱ)略(Ⅲ)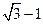
(Ⅰ)由题设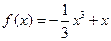 ,∴
,∴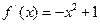 ,由于点(2,2)不在曲线G上,
,由于点(2,2)不在曲线G上,
可设切点为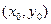 ,所求切线方程为
,所求切线方程为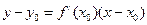 ,由
,由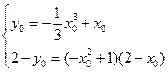 ,消去
,消去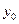 得
得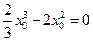 ,∴
,∴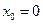 ,或
,或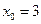 ,即对应的切点为(0,0),或
,即对应的切点为(0,0),或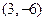 ,
,
当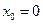 时,
时,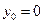 ,
,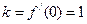 ,所求的切线方程为
,所求的切线方程为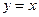 ,…2分
,…2分
当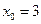 时,
时,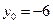 ,
,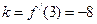 ,所求切线方程为
,所求切线方程为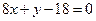 ;…4分
;…4分
(Ⅱ)由已知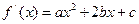 ,依题意有
,依题意有
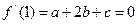 ,
,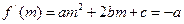 ,即
,即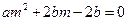 ,
,
从而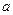 、
、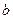 、
、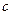 三数中至少有一个正数一个负数,∴总有
三数中至少有一个正数一个负数,∴总有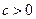 ,
,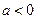 ,
,
若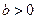 ,由
,由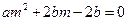 有
有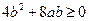 ,∴
,∴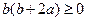 ,∴
,∴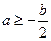 ,
,
又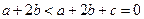 ,∴
,∴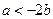 ,故得
,故得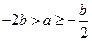 ,从而
,从而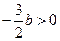 ,
,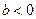 矛盾,
矛盾,
∴必有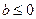 ,∴
,∴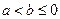 ,∴可得
,∴可得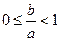 ;………8分
;………8分
(Ⅲ)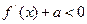 即
即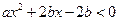 ,整理即得
,整理即得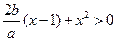 ,设
,设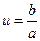 ,则
,则
设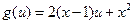 为
为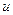 的函数,由条件(Ⅱ),欲不等式
的函数,由条件(Ⅱ),欲不等式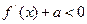 恒成立,即
恒成立,即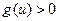 在
在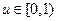 时恒成立,∴
时恒成立,∴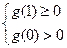 ,∴
,∴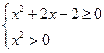 ,解得
,解得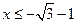 ,或
,或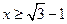 ,
,
依题意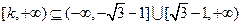 ,∴
,∴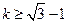 ,即所求的
,即所求的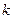 的最小值为
的最小值为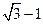 .
.
本题综合考查曲线的概念、一次函数的性质、导数的几何意义、不等式的解法与证明,属难题.
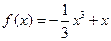 ,∴
,∴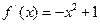 ,由于点(2,2)不在曲线G上,
,由于点(2,2)不在曲线G上,可设切点为
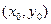 ,所求切线方程为
,所求切线方程为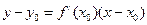 ,由
,由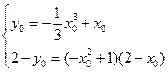 ,消去
,消去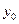 得
得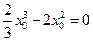 ,∴
,∴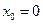 ,或
,或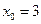 ,即对应的切点为(0,0),或
,即对应的切点为(0,0),或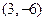 ,
,当
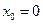 时,
时,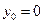 ,
,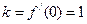 ,所求的切线方程为
,所求的切线方程为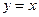 ,…2分
,…2分当
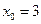 时,
时,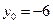 ,
,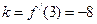 ,所求切线方程为
,所求切线方程为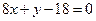 ;…4分
;…4分(Ⅱ)由已知
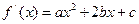 ,依题意有
,依题意有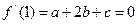 ,
,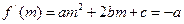 ,即
,即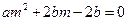 ,
,从而
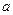 、
、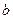 、
、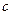 三数中至少有一个正数一个负数,∴总有
三数中至少有一个正数一个负数,∴总有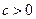 ,
,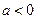 ,
,若
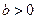 ,由
,由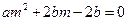 有
有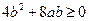 ,∴
,∴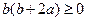 ,∴
,∴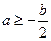 ,
,又
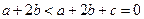 ,∴
,∴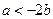 ,故得
,故得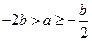 ,从而
,从而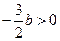 ,
,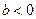 矛盾,
矛盾,∴必有
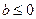 ,∴
,∴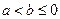 ,∴可得
,∴可得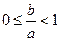 ;………8分
;………8分(Ⅲ)
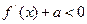 即
即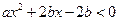 ,整理即得
,整理即得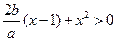 ,设
,设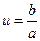 ,则
,则设
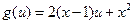 为
为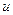 的函数,由条件(Ⅱ),欲不等式
的函数,由条件(Ⅱ),欲不等式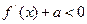 恒成立,即
恒成立,即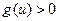 在
在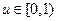 时恒成立,∴
时恒成立,∴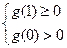 ,∴
,∴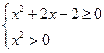 ,解得
,解得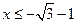 ,或
,或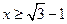 ,
,依题意
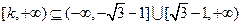 ,∴
,∴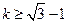 ,即所求的
,即所求的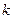 的最小值为
的最小值为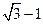 .
.本题综合考查曲线的概念、一次函数的性质、导数的几何意义、不等式的解法与证明,属难题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
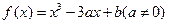 .(Ⅰ)若曲线
.(Ⅰ)若曲线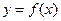 在点
在点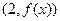 处与直线
处与直线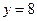 相切,求
相切,求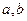 的值;(Ⅱ)求函数
的值;(Ⅱ)求函数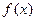 的单调区间与极值点.
的单调区间与极值点.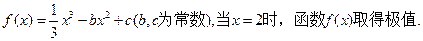
 的单调区间;(Ⅱ)若函数
的单调区间;(Ⅱ)若函数
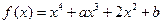 (
(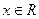 ),其中
),其中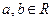 .(Ⅰ)当
.(Ⅰ)当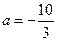 时,讨论函数
时,讨论函数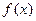 的单调性;(Ⅱ)若函数
的单调性;(Ⅱ)若函数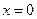 处有极值,求
处有极值,求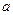 的取值范围;(Ⅲ)若对于任意的
的取值范围;(Ⅲ)若对于任意的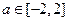 ,不等式
,不等式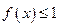 在
在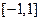 上恒成立,求
上恒成立,求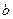 的取值范围.
的取值范围.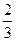 x3-2ax2+3x(x∈R).
x3-2ax2+3x(x∈R). 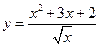 ,则
,则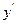 等于( )
等于( )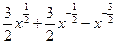

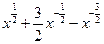
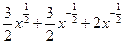
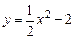 在点
在点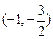 处的切线为
处的切线为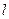 ,则
,则 ,若,
,若,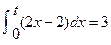 ,则
,则 。
。