题目内容
15.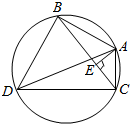 如图,AD是圆O的直径,AE⊥BC,且AB=3,AC=2,AD=6.
如图,AD是圆O的直径,AE⊥BC,且AB=3,AC=2,AD=6.(1)求证:AB•AC=AD•AE;
(2)求BE的值.
分析 (1)利用两个对应角相等可以证明三角形相似,再根据相似三角形的性质得出比例证明;
(2)求出AE=1,CD=4$\sqrt{2}$,可得tan∠ADC=$\frac{\sqrt{2}}{4}$,tan∠ABE=$\frac{\sqrt{2}}{4}$,即可求BE的值.
解答 (1)证明:由圆周角定理可知,∠ACE=∠ADB,
∵AD是圆O的直径,AE⊥BC,
∴∠ABD=∠AEC=90°,
∴△ADB∽△ACE.
∴AB:AE=AD:AC,
∴AB•AC=AE•AD.
(2)解:∵AB=3,AC=2,AD=6,AB•AC=AE•AD
∴AE=1,CD=4$\sqrt{2}$,
∴tan∠ADC=$\frac{\sqrt{2}}{4}$,
∴tan∠ABE=$\frac{\sqrt{2}}{4}$,
∴$\frac{1}{BE}$=$\frac{\sqrt{2}}{4}$,
∴BE=2$\sqrt{2}$.
点评 乘积的形式通常可以转化成比例的形式,通过证明三角形相似得出结论.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
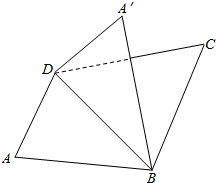 已知ABCD是直角梯形,AB=AD,AD∥BC,AB⊥BC,CD⊥BD,把△ABD沿BD折起,使平面A′BD⊥面BCD.
已知ABCD是直角梯形,AB=AD,AD∥BC,AB⊥BC,CD⊥BD,把△ABD沿BD折起,使平面A′BD⊥面BCD.
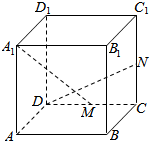 如图,在正方体ABCD-A1B1C1D1中,M,N分别是CD,CC1的中点,给出下列命题:
如图,在正方体ABCD-A1B1C1D1中,M,N分别是CD,CC1的中点,给出下列命题: