题目内容
3.设函数f(x)=log2x-logx4(0<x<1),数列{an}的通项an满足f(2${\;}^{{a}_{n}}$)=2n(n∈N+).(1)求数列{an}的通项公式;
(2)证明:数列{an}为递增数列.
分析 (1)由对数的性质,可得f(x)=log2x-$\frac{2}{lo{g}_{2}x}$,由条件,可得an2-2nan-2=0,解方程即可得到所求通项;
(2)运用分子有理化,化简an,再比较an+1与an的大小关系,即可得证.
解答 解:(1)f(x)=log2x-logx4=log2x-$\frac{2}{lo{g}_{2}x}$,
f(2${\;}^{{a}_{n}}$)=2n(n∈N+).
即log2${2}^{{a}_{n}}$-$\frac{2}{lo{g}_{2}{2}^{{a}_{n}}}$=2n,
即有an2-2nan-2=0,此时0<2${\;}^{{a}_{n}}$<1,an<0,
∴an=n-$\sqrt{{n}^{2}+2}$;
(2)证明:an=n-$\sqrt{{n}^{2}+2}$=-$\frac{2}{\sqrt{{n}^{2}+2}+n}$,
an+1=-$\frac{2}{\sqrt{(n+1)^{2}+2}+(n+1)}$,
由于$\sqrt{{n}^{2}+2}$+n是递增数列,
即有$\sqrt{(n+1)^{2}+2}$+(n+1)>$\sqrt{{n}^{2}+2}$+n,
则$\frac{2}{\sqrt{(n+1)^{2}+2}+(n+1)}$<$\frac{2}{\sqrt{{n}^{2}+2}+n}$,
即有an+1>an,
则数列{an}为递增数列.
点评 本题考查数列的通项的求法,注意运用方程的思想,考查数列单调性的判断,注意数列相邻两项大小的比较,属于中档题.

练习册系列答案
相关题目
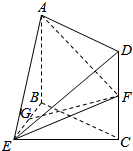 如图所示,在四较锥E-ABCD中,底面ABCD为矩形,CD⊥平面BEC,G是线段BE上一点,F是线段DC的中点且GF∥平面ADE,AB=BE=EC=2.
如图所示,在四较锥E-ABCD中,底面ABCD为矩形,CD⊥平面BEC,G是线段BE上一点,F是线段DC的中点且GF∥平面ADE,AB=BE=EC=2.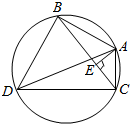 如图,AD是圆O的直径,AE⊥BC,且AB=3,AC=2,AD=6.
如图,AD是圆O的直径,AE⊥BC,且AB=3,AC=2,AD=6.