题目内容
2.已知函数y=a+$\sqrt{-{x}^{2}+ax-b}$的值域为[4,7],求a,b的值.分析 化简可求得a=4,再由-(x-2)2+4-b的最大值为9知4-b=9,从而解得.
解答 解:∵a+$\sqrt{-{x}^{2}+ax-b}$≥a,
∴a=4,
∴$\sqrt{-{x}^{2}+ax-b}$的最大值为7-4=3,
∴-(x-2)2+4-b的最大值为9,
即4-b=9,
故b=-5.
点评 本题考查了函数的值域的求法,属于基础题.

练习册系列答案
相关题目
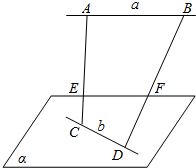 如图所示,a,b是异面直线,A,B∈a,C,D∈b,E,F分别为线段AC,BD的中点,判断直线EF和a的位置关系,并证明你的结论.
如图所示,a,b是异面直线,A,B∈a,C,D∈b,E,F分别为线段AC,BD的中点,判断直线EF和a的位置关系,并证明你的结论.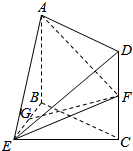 如图所示,在四较锥E-ABCD中,底面ABCD为矩形,CD⊥平面BEC,G是线段BE上一点,F是线段DC的中点且GF∥平面ADE,AB=BE=EC=2.
如图所示,在四较锥E-ABCD中,底面ABCD为矩形,CD⊥平面BEC,G是线段BE上一点,F是线段DC的中点且GF∥平面ADE,AB=BE=EC=2.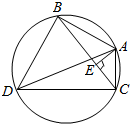 如图,AD是圆O的直径,AE⊥BC,且AB=3,AC=2,AD=6.
如图,AD是圆O的直径,AE⊥BC,且AB=3,AC=2,AD=6.