题目内容
3.关于函数f(x)=4sin(2x+$\frac{π}{3}$)(x∈R)有如下说法:①由f(x1)=f(x2)=0可得,x1-x2是π的整数倍;
②表达式可改写为f(x)=4cos(2x-$\frac{π}{6}$);
③函数的图象关于点(-$\frac{π}{6}$,0)对称;
④函数的图象关于直线x=-$\frac{π}{6}$对称;
⑤函数在区间[-$\frac{5π}{12}$,$\frac{π}{12}$]上是减函数;
⑥函数为奇函数.其中你认为所有正确的说法的序号是②③.
分析 由正弦函数的周期性判断①;由诱导公式判断②;由正弦函数的对称性判断③、④;由正弦函数的单调性和整体思想判断⑤;由奇函数的定义判断⑥.
解答 解:①由f(x1)=f(x2)=0得,x1-x2是半个周期的整数倍也成立,
又f(x)=4sin(2x+$\frac{π}{3}$)的周期是π,①不正确;
②因为2x+$\frac{π}{3}$=2x+$\frac{π}{2}-\frac{π}{6}$,所以f(x)=4sin(2x+$\frac{π}{3}$)=4cos(2x-$\frac{π}{6}$),②正确;
③当x=-$\frac{π}{6}$时,2x+$\frac{π}{3}$=0,则f(-$\frac{π}{6}$)=0,所以函数的图象关于点(-$\frac{π}{6}$,0)对称,③正确;
④由③可得函数的图象不关于直线x=-$\frac{π}{6}$对称,④不正确;
⑤由x∈[-$\frac{5π}{12}$,$\frac{π}{12}$]得,2x+$\frac{π}{3}$∈[-$\frac{π}{2}$,$\frac{π}{2}$],则函数f(x)在区间[-$\frac{5π}{12}$,$\frac{π}{12}$]上是增函数,⑤不正确;
⑥因为f(-x)=4sin(-2x+$\frac{π}{3}$)≠-f(x),则f(x)=4sin(2x+$\frac{π}{3}$)不是奇函数,⑥不正确,
综上可得,正确的命题是:②③,
故答案为:②③.
点评 本题考查命题的真假性判断,以及正弦函数的对称性、周期性,诱导公式的应用,掌握正弦函数的图象性质是解题的关键,属于中档题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
13.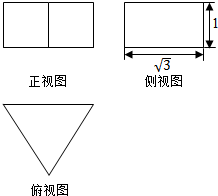 若正三棱柱(底面为正三角形,且侧棱与底面垂直的三棱柱)的三视图如图所示,该三棱柱的表面积是( )
若正三棱柱(底面为正三角形,且侧棱与底面垂直的三棱柱)的三视图如图所示,该三棱柱的表面积是( )
 若正三棱柱(底面为正三角形,且侧棱与底面垂直的三棱柱)的三视图如图所示,该三棱柱的表面积是( )
若正三棱柱(底面为正三角形,且侧棱与底面垂直的三棱柱)的三视图如图所示,该三棱柱的表面积是( )| A. | $\sqrt{3}$ | B. | 6+2$\sqrt{3}$ | C. | 6+$\sqrt{3}$ | D. | $\frac{9\sqrt{3}}{2}$ |
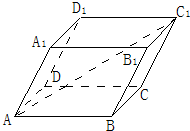 已知平行六面体,AB=AD=AA1=1,∠BAD=∠BAA1=∠DAA1=60°,求|$\overrightarrow{A{C}_{1}}$|.
已知平行六面体,AB=AD=AA1=1,∠BAD=∠BAA1=∠DAA1=60°,求|$\overrightarrow{A{C}_{1}}$|.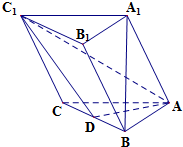 如图,在三棱柱ABC-A1B1C1中,D为棱BC的中点,AB⊥BC,BC⊥BB1,AB=A1B=1,BB1=$\sqrt{2}$.求证:
如图,在三棱柱ABC-A1B1C1中,D为棱BC的中点,AB⊥BC,BC⊥BB1,AB=A1B=1,BB1=$\sqrt{2}$.求证: