题目内容
【题目】已知椭圆![]() :
: ![]() 的右顶点、上顶点分别为
的右顶点、上顶点分别为![]() 、
、![]() ,坐标原点到直线
,坐标原点到直线![]() 的距离为
的距离为![]() ,且
,且![]() ,则椭圆
,则椭圆![]() 的方程为( )
的方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
写出直线![]() 的方程,利用原点到直线
的方程,利用原点到直线![]() 的距离,以及
的距离,以及![]() 列方程组,解方程组求得
列方程组,解方程组求得![]() 的值,进而求得椭圆的方程.
的值,进而求得椭圆的方程.
椭圆右顶点坐标为![]() ,上顶点坐标为
,上顶点坐标为![]() ,故直线
,故直线![]() 的方程为
的方程为![]() ,即
,即![]() ,依题意原点到直线的距离为
,依题意原点到直线的距离为![]() ,且
,且![]() ,由此解得
,由此解得![]() ,故椭圆的方程为
,故椭圆的方程为![]() ,故选D.
,故选D.
【点睛】
本小题主要考查过两点的直线方程,考查点到直线的距离公式,考查椭圆标准方程的求法,考查了方程的思想.属于中档题.
【题型】单选题
【结束】
11
【题目】若实数![]() ,
,![]() 满足
满足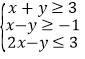 ,则
,则![]() 的最小值是( )
的最小值是( )
A. 0 B. ![]() C. -6 D. -3
C. -6 D. -3
【答案】C
【解析】
画出可行域,向上平移目标函数![]() 到可行域边界的位置,由此求得目标函数的最小值.
到可行域边界的位置,由此求得目标函数的最小值.
画出可行域如下图所示,由图可知,目标函数![]() 在点
在点![]() 处取得最小值为
处取得最小值为![]() .故选C.
.故选C.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目