题目内容
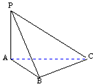
如图,正方体ABCD-A1B1C1D1中,点E在棱CD上.
(1)求证:EB1⊥AD1;
(2)若E是CD中点,求EB1与平面AD1E所成的角;
(3)设M在BB1上,且
=
,是否存在点E,使平面AD1E⊥平面AME,若存在,指出点E的位置,若不存在,请说明理由.

(1)求证:EB1⊥AD1;
(2)若E是CD中点,求EB1与平面AD1E所成的角;
(3)设M在BB1上,且
| BM |
| MB1 |
| 2 |
| 3 |

以D为坐标原点,DA,DC,DD1依次为x轴、y轴,z轴正方向建立空间直角坐标系,
并设正方体棱长为1,设点E的坐标为E(0,t,0)
(1)
=(-1,0,1),
=(1,1-t,1)
∵
•
=0,
∴EB1⊥AD1
(2)当E是CD中点时,
=(-1,0,1),
=(-1,
,0),
设平面AD1E的一个法向量是
=(x,y,z),
则由
•
=0,
•
=0
得一组解是
=(1,2,1),
又
=(1,1-t,1),由cosθ=
=
,
从而直线EB1与平面AD1E所成的角的正弦值是
(3)设存在符合题意的E点为E(0,t,0)可得平面AD1E的一个法向量是
=(t,1,t),
平面AME的一个法向量是
=(t,1,-
)
∵平面AD1E⊥平面AME,
∴
•
=t2+1-
t=0,
解得t=
或t=2(舍),
故当点E是CD的中点时,平面AD1E⊥平面AME
并设正方体棱长为1,设点E的坐标为E(0,t,0)
(1)
| AD1 |
| EB1 |
∵
| AD1 |
| EB1 |
∴EB1⊥AD1
(2)当E是CD中点时,
| AD1 |
| AE |
| 1 |
| 2 |
设平面AD1E的一个法向量是
| n |
则由
| AD1 |
| n |
| AE |
| n |
得一组解是
| n |
又
| EB1 |
| ||||
|
|
| ||
| 3 |
从而直线EB1与平面AD1E所成的角的正弦值是
| ||
| 3 |
(3)设存在符合题意的E点为E(0,t,0)可得平面AD1E的一个法向量是
| a |
平面AME的一个法向量是
| b |
| 5 |
| 2 |
∵平面AD1E⊥平面AME,
∴
| a |
| b |
| 5 |
| 2 |
解得t=
| 1 |
| 2 |
故当点E是CD的中点时,平面AD1E⊥平面AME

练习册系列答案
相关题目
 平面β,给出下列命题:
平面β,给出下列命题: 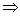 l∥M;
l∥M;