题目内容
已知函数 是首项为2,公比为
是首项为2,公比为 的等比数列,数列
的等比数列,数列 是首项为-2,第三项为2的等差数列.
是首项为-2,第三项为2的等差数列.
(1)求数列 的通项式.
的通项式.
(2)求数列 的前
的前 项和
项和 .
.
 是首项为2,公比为
是首项为2,公比为 的等比数列,数列
的等比数列,数列 是首项为-2,第三项为2的等差数列.
是首项为-2,第三项为2的等差数列.(1)求数列
 的通项式.
的通项式.(2)求数列
 的前
的前 项和
项和 .
.(1) ,bn=2n-4-
,bn=2n-4-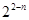 ; (2)Tn=n2-3n-4+
; (2)Tn=n2-3n-4+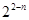 .
.
 ,bn=2n-4-
,bn=2n-4-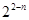 ; (2)Tn=n2-3n-4+
; (2)Tn=n2-3n-4+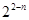 .
.试题分析:(1)直接用等比数列等差数列即可求得数列{
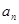 }{bn}的通项公式.
}{bn}的通项公式.(2)数列
 是一个等差数列与一个等比数列的和,故其求和采用分组求和的方法.
是一个等差数列与一个等比数列的和,故其求和采用分组求和的方法.试题解析:(1)∵数列{
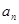 }是首项
}是首项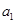 =2,公比q=
=2,公比q=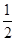 的等比数列,
的等比数列,∴an=2·
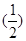 n-1=22-n,
n-1=22-n,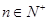 3分
3分依题意得数列{bn+an}的公差d=
 =2,
=2,∴bn+an=-2+2(n-1)=2n-4,
∴bn=2n-4-22-n,
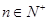 6分
6分(2)设Sn为
 的前n项和,由(1)得 Sn=
的前n项和,由(1)得 Sn=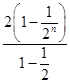 =4
=4 9分
9分设数列{bn+an}的前n项和为Pn 则 Pn=
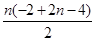 =n(n-3),
=n(n-3),∴Tn=Pn-Sn=n(n-3)-4
 =n2-3n-4+22-n 12分
=n2-3n-4+22-n 12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,数列
,数列 的前
的前 项和为
项和为 ,点
,点 均在函数
均在函数 的图象上.
的图象上. ;
;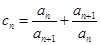 ,证明:
,证明: .
.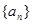 的前
的前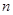 项和
项和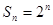 ,数列
,数列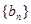 满足
满足
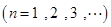 .
.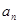 ;(Ⅱ)求数列
;(Ⅱ)求数列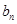 ;
;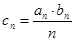 ,求数列
,求数列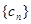 的前
的前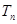 .
. (
( )那么
)那么 共有 项.
共有 项.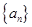 满足
满足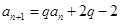 (
(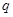 为常数,
为常数,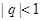 ),若
),若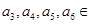
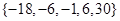 ,则
,则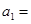 .
. ,cn+1=
,cn+1= ,则( )
,则( ) ,则
,则 是这个数列的 ( )
是这个数列的 ( ) 项
项 项
项 项
项 项
项 ,[ an]表示an的整数部分,(an)表示an的小数部分,an+1="[" an]+
,[ an]表示an的整数部分,(an)表示an的小数部分,an+1="[" an]+ (
( ),数列{bn}中,b1=1,b2=2,
),数列{bn}中,b1=1,b2=2, (
( ),则a1b1+ a2b2+…+anbn=
),则a1b1+ a2b2+…+anbn=