题目内容
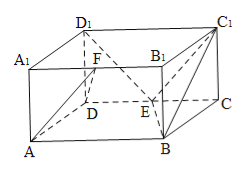
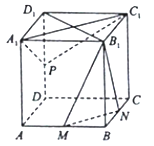
【题目】如图,正方体![]() 中,
中,![]() 分别为
分别为![]() 的中点.
的中点.
(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)当点![]() 在
在![]() 上运动时,是否都有
上运动时,是否都有![]() 平面
平面![]() ,证明你的结论;
,证明你的结论;
(3)若![]() 是
是![]() 的中点,求
的中点,求![]() 与
与![]() 所成的角的余弦值.
所成的角的余弦值.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】试题分析:(1)连接AC,由正方形性质得AC⊥BD,又由正方体ABCD-A1B1C1D1中,M,N分别是AB,BC的中点,易得MN∥AC,则MN⊥BD.BB1⊥MN,由线面垂直的判定定理,可得MN⊥平面BB1D1D,进而由面面垂直的判定定理,可得平面B1MN⊥平面BB1D1D;
(2)当点P在DD1上移动时,都有MN∥平面A1C1P.由线面平行的判定定理证明即可;
(3)设C1 C的中点为G,连接PG,B1G,即可说明∠GB1N即为A1P与B1N所成的角,在△GB1N中利用余弦定理求解即可.
试题解析:
(1)正方体![]() 中,
中,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() ,
,
连接![]() ,因为
,因为![]() 分别为
分别为![]() 的中点,
的中点,
所以![]() ,
,
又四边形![]() 是正方形,所以
是正方形,所以![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
(2)当点![]() 在
在![]() 上移动时,都有
上移动时,都有![]() 平面
平面![]() ,证明如下:
,证明如下:
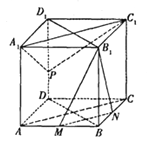
在正方体中![]() ,A1A∥C1C,且A1A=C1C,所以A1ACC1为平行四边形,
,A1A∥C1C,且A1A=C1C,所以A1ACC1为平行四边形,
在正方体中![]() ,A1A∥C1C,且A1A=C1C,所以A1ACC1为平行四边形,
,A1A∥C1C,且A1A=C1C,所以A1ACC1为平行四边形,
所以A1 C1∥A C,
由(1)知,MN∥A C,所以MN∥A1 C1 又![]()
所以![]() ]
]
(3)设C1 C的中点为G,连接PG,B1G
又因为P是D1D的中点,所以PG∥C1D1且PG=C1D1,又A1B1∥C1D1且A1B1=C1D1
所以四边形A1B1GP为平行四边形,故A1P∥B1G且A1P=B1G
所以∠GB1N即为A1P与B1N所成的角
设正方体的棱长为2,所以在△GB1N中,B1G= B1N=![]() ,GN=
,GN=![]()
所以cos∠GB1N=![]() .
.

练习册系列答案
相关题目