题目内容
【题目】已知函数![]() ,
,![]() ,
,![]() ,其中
,其中![]() 为正实数,
为正实数,![]() 为自然对数的底数.
为自然对数的底数.
(1)求函数![]() 的单调区间;
的单调区间;
(2)是否存在实数![]() ,使得对任意给定的
,使得对任意给定的![]() ,在区间
,在区间![]() 上总存在两个不同的
上总存在两个不同的![]() ,
,![]() ,使得
,使得![]() 成立?若存在,求出正实数
成立?若存在,求出正实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1)函数![]() 的单调递增区间为
的单调递增区间为![]() 与
与![]() ,单调递减区间为
,单调递减区间为![]() 与
与![]() ;(2)存在,
;(2)存在,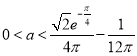 .
.
【解析】
(1)求出导函数![]() ,由
,由![]() 确定增区间,由
确定增区间,由![]() 确定减区间;
确定减区间;
(2)由(1)求出![]() 的图象与
的图象与![]() 在区间
在区间![]() 上至少有两个交点的
上至少有两个交点的![]() 的取值范围,函数
的取值范围,函数![]() 的值域就是这个范围的子集.由此可得.
的值域就是这个范围的子集.由此可得.
解:(1)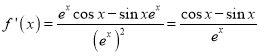 ,
,![]() .
.
当![]() ,即
,即![]() 时,
时,![]() 或
或![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() 或
或![]() .
.
∴函数![]() 的单调递增区间为
的单调递增区间为![]() 与
与![]() ,单调递减区间为
,单调递减区间为![]() 与
与![]() .
.
(2)由(1)可知,函数![]() 有两个极小值,
有两个极小值,![]() ,
,![]() ,
,
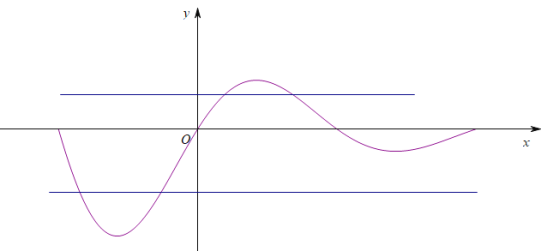
存在一个极大值![]() 大致作出函数图像(只反映单调性)可知:
大致作出函数图像(只反映单调性)可知:
对于函数![]() ,
,![]() ,假设存在满足题意的实数
,假设存在满足题意的实数![]() .
.
当![]() 时,由
时,由![]() ,得
,得![]() .
.
由题意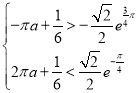 ,解得
,解得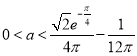 .
.
所以,实数![]() 的取值范围是
的取值范围是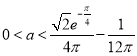 .
.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案
相关题目
【题目】据长期统计分析,某货物每天的需求量![]() 在17与26之间,日需求量
在17与26之间,日需求量![]() (件)的频率
(件)的频率![]() 分布如下表所示:
分布如下表所示:
需求量 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
频率 | 0.12 | 0.18 | 0.23 | 0.13 | 0.10 | 0.08 | 0.05 | 0.04 | 0.04 | 0.03 |
已知其成本为每件5元,售价为每件10元.若供大于求,则每件需降价处理,处理价每件2元.假设每天的进货量必需固定.
(1)设每天的进货量为![]() ,视日需求量
,视日需求量![]() 的频率为概率
的频率为概率![]() ,求在每天进货量为
,求在每天进货量为![]() 的条件下,日销售量
的条件下,日销售量![]() 的期望值
的期望值![]() (用
(用![]() 表示);
表示);
(2)在(1)的条件下,写出![]() 和
和![]() 的关系式,并判断
的关系式,并判断![]() 为何值时,日利润的均值最大?
为何值时,日利润的均值最大?