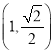题目内容
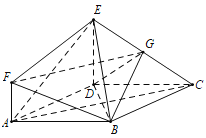
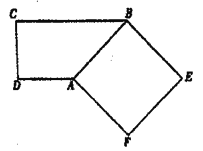
【题目】如图1,梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 翻折,构成一个四棱锥
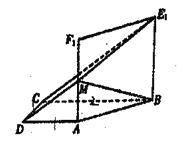
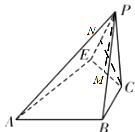
翻折,构成一个四棱锥![]() ,如图2.
,如图2.
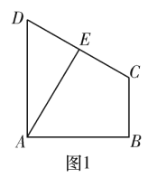
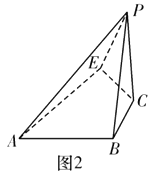
(1)求证:异面直线![]() 与
与![]() 垂直;
垂直;
(2)求直线![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(3)若三棱锥![]() 的体积为
的体积为![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析(2)60°(3)![]()
【解析】
(1)取![]() 中点
中点![]() ,连接
,连接![]() ,通过证明
,通过证明![]() 平面
平面![]() ,可得
,可得![]() ;
;
(2)由(1)可得![]() 为直线
为直线![]() 与平面
与平面![]() 所成角,求出即可;
所成角,求出即可;
(3)证明![]() 平面
平面![]() ,可得
,可得![]() ,可得
,可得![]() ,进而可得
,进而可得![]() 为等边三角形,则可得
为等边三角形,则可得![]() 平面
平面![]() ,求出
,求出![]() 即可.
即可.
(1)在图1中,取![]() 中点
中点![]() ,连接
,连接![]() ,由已知,得四边形
,由已知,得四边形![]() 为矩形,且
为矩形,且![]() ,得
,得![]() ,
,
则![]() 为等边三角形,故
为等边三角形,故![]() ,
,
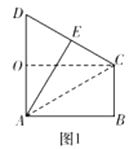
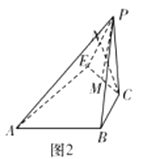
故图2中,![]() ,又
,又![]() 与
与![]() 是相交直线,
是相交直线,
得![]() 平面
平面![]() ,则
,则![]() .
.
(2)由(1),得![]() 平面
平面![]() ,则直线
,则直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
即直线![]() 与平面
与平面![]() 所成角为60°.
所成角为60°.
(3)在平面![]() 内做
内做![]() ,交
,交![]() 于
于![]() ,
,
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
又平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,
,
![]() 平面
平面![]() .
.
![]() ,
,
∴![]() ,
,
∴![]() .
.
![]() 中,
中,![]() ,则
,则![]() ,
,
故![]() 为等边三角形.在
为等边三角形.在![]() 内作
内作![]() ,交
,交![]() 于
于![]() ,
,
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,又平面
,又平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,
,
∴![]() 平面
平面![]() ,∵
,∵![]() ,∴点
,∴点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目