题目内容
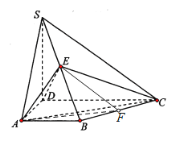
【题目】如图,四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为棱
为棱![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离,
的距离,
【答案】(1)见证明;(2) ![]()
【解析】
(1)取![]() 的中点
的中点![]() ,则
,则![]() ,通过勾股证得
,通过勾股证得![]() 即得
即得![]() 结合
结合![]() 即可得证.
即可得证.
(2)先求![]() 再求
再求![]() 根据体积公式
根据体积公式![]() 计算即可.
计算即可.
解:(1)取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]() .如图:
.如图:
因为![]() 底面
底面![]() 所以
所以![]() ,
,
又因为![]() 且
且![]() ,
,
所以![]() 平面
平面![]() ,得
,得![]() .
.
又因为![]() 面
面![]() 且
且![]() 所以
所以![]() 面
面![]() ,
,
在![]() SAD中
SAD中![]() ,
,
在![]() SAB中
SAB中![]() ,
,![]() 为
为![]() 的中点,故
的中点,故![]() ,
,
在![]() 中
中![]() ,所以
,所以![]() ,
,
在![]() 中,
中,![]() ,故
,故![]() ,在
,在![]() 中,
中,![]() ,故
,故![]() ,在
,在![]() 中,
中,![]() ,由余弦定理知
,由余弦定理知![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() 满足勾股定理所以
满足勾股定理所以![]() ,从而
,从而![]() .
.
所以![]() 平面
平面![]() .
.
(2)连接BD并取中点O,连接EO,OC,过O作![]() 交CD于M点,过O作
交CD于M点,过O作![]() 交AD于N点,如图:
交AD于N点,如图:

![]() 在
在![]() 中,
中,![]() ,
,![]() ,
,![]()
![]()

![]()
![]() 底面
底面![]() 且
且![]() 为棱
为棱![]() 的中点
的中点
![]()
![]() 底面
底面![]() 即
即![]() 为直角三角形即
为直角三角形即
在![]() 中
中![]() ,
,![]() ,
,![]() 由余弦定理知
由余弦定理知![]() 即
即![]()
![]()
![]() .
.
![]()
![]() ,且
,且![]() ,
,
![]()
![]() ,解得
,解得![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
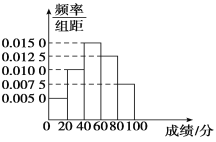
【题目】某中学准备组建“文科”兴趣特长社团,由课外活动小组对高一学生文科、理科进行了问卷调查,问卷共100道题,每题1分,总分100分,该课外活动小组随机抽取了200名学生的问卷成绩(单位:分)进行统计,将数据按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成5组,绘制的频率分布直方图如图所示,若将不低于60分的称为“文科方向”学生,低于60分的称为“理科方向”学生.
分成5组,绘制的频率分布直方图如图所示,若将不低于60分的称为“文科方向”学生,低于60分的称为“理科方向”学生.
|
|
(1)根据已知条件完成下面![]() 列联表,并据此判断是否有99%的把握认为是否为“文科方向”与性别有关?
列联表,并据此判断是否有99%的把握认为是否为“文科方向”与性别有关?
(2)将频率视为概率,现在从该校高一学生中用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中“文科方向”的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列、期望
的分布列、期望![]() 和方差
和方差![]() .
.
参考公式: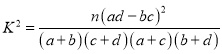 ,其中
,其中![]() .
.
参考临界值:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |