题目内容
【题目】已知直线l：y＝3x＋3，求：
(1)点P(4,5)关于直线l的对称点坐标；
(2)直线l1：y＝x－2关于直线l的对称直线的方程；
(3)直线l关于点A(3,2)的对称直线的方程．
【答案】(1) P′(－2,7);(2) 7x＋y＋22＝0;(3) 3x－y－17＝0.
【解析】试题分析:(1) 设点P关于直线l的对称点为P′(x′，y′)，则线段PP′的中点M在直线l上，且直线PP′垂直于直线l，列出方程组求出坐标即可;(2)法一:联立两直线方程求出交点坐标; 在直线l1：x－y－2＝0上任取一点(2,0)，过点(2,0)与直线l：3x－y＋3＝0垂直的直线方程为x＋3y＝2,联立两直线方程求出交点坐标;根据两个交点坐标利用两点式方程写出直线;法二: 在直线l1上任取一点P(x1，y1),根据点P关于直线l的对称点为Q(x′，y′), 列出方程组把P点坐标用x′，y′表示,又点P在直线l1上运动，代入整理即可;(3) 设直线l关于点A(3,2)的对称直线为l′，根据直线平行设出方程, 任取y＝3x＋3上的一点(0,3)，则该点关于点A(3,2)的对称点一定在直线l′上，将解出的对称点代入直线方程,求出纵截距,可得直线方程.
试题解析:
(1)设点P关于直线l的对称点为P′(x′，y′)，则线段PP′的中点M在直线l上，且直线PP′垂直于直线l，
即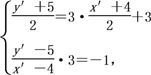
解得
.
所以P′(－2,7)．
(2)法一：联立方程组
解得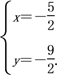
所以直线l1与l的交点为
.
在直线l1：x－y－2＝0上任取一点(2,0)，过点(2,0)与直线l：3x－y＋3＝0垂直的直线方程为x＋3y＝2.
设直线x＋3y＝2与直线l的交点坐标为(x0，y0)，
则
解得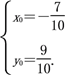
即交点坐标为
.
又点(2,0)关于点对称的点的坐标为
，
所以过两点，的直线方程为
＝
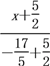，整理，得7x＋y＋22＝0.
则所求直线方程为7x＋y＋22＝0.
法二：在直线l1上任取一点P(x1，y1)(P∈l1)，设点P关于直线l的对称点为Q(x′，y′)，则
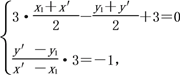
解得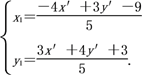
又点P在直线l1上运动，所以x1－y1－2＝0.
所以
－
－2＝0，
即 7x′＋y′＋22＝0.
所以所求直线方程为7x＋y＋22＝0.
(3)设直线l关于点A(3,2)的对称直线为l′，
由l∥l′，设l′：y′＝3x′＋b.
任取y＝3x＋3上的一点(0,3)，则该点关于点A(3,2)的对称点一定在直线l′上，设其对称点为(x′，y′)．
则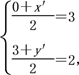
解得
代入y′＝3x′＋b，得b＝－17.
故直线l′的方程为y′＝3x′－17，
即所求直线的方程为3x－y－17＝0.
点睛: 三种对称(1)点关于点的对称：点P(x0，y0)关于A(a，b)的对称点为P′(2a－x0,2b－y0)．(2)点关于直线的对称：设点P(x0，y0)关于直线y＝kx＋b的对称点P′(x′，y′)，
则有两直线斜率乘积为-1,且两点中点在直线上,可求出x′，y′.(3)直线关于直线的对称：①若直线l1与对称轴l相交，则交点必在与l1对称的直线l2上，然后再求出l1上任一个已知点P1关于对称轴l对称的点P2，那么经过交点及点P2的直线就是l2；②若直线l1与对称轴l平行，则与l1对称的直线和l1分别到直线l的距离相等，由平行直线系和两条平行线间的距离即可求出l1的对称直线．
