题目内容
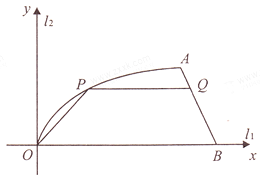
【题目】设椭圆 ![]() +
+ ![]() =1(a>b>0)的左、右焦点分别为F1、F2 , 右顶点为A,上顶点为B,已知|AB|=
=1(a>b>0)的左、右焦点分别为F1、F2 , 右顶点为A,上顶点为B,已知|AB|= ![]() |F1F2|.
|F1F2|.
(1)求椭圆的离心率;
(2)设P为椭圆上异于其顶点的一点,以线段PB为直径的圆经过点F1 , 经过原点O的直线l与该圆相切,求直线l的斜率.
【答案】
(1)解:设椭圆的右焦点为F2(c,0),
由|AB|= ![]() |F1F2|,可得
|F1F2|,可得 ![]() ,化为a2+b2=3c2.
,化为a2+b2=3c2.
又b2=a2﹣c2,∴a2=2c2.
∴e= ![]() .
.
(2)解:由(1)可得b2=c2.因此椭圆方程为 ![]() .
.
设P(x0,y0),由F1(﹣c,0),B(0,c),可得 ![]() =(x0+c,y0),
=(x0+c,y0), ![]() =(c,c).
=(c,c).
∵ ![]() ,
,
∴ ![]() =c(x0+c)+cy0=0,
=c(x0+c)+cy0=0,
∴x0+y0+c=0,
∵点P在椭圆上,∴ ![]() .
.
联立 ![]() ,化为
,化为 ![]() =0,
=0,
∵x0≠0,∴ ![]() ,
,
代入x0+y0+c=0,可得 ![]() .
.
∴P ![]() .
.
设圆心为T(x1,y1),则 ![]() =﹣
=﹣ ![]() ,
, ![]() =
= ![]() .
.
∴T ![]() ,
,
∴圆的半径r= ![]() =
= ![]() .
.
设直线l的斜率为k,则直线l的方程为:y=kx.
∵直线l与圆相切,
∴ ![]() ,
,
整理得k2﹣8k+1=0,解得 ![]() .
.
∴直线l的斜率为 ![]() .
.
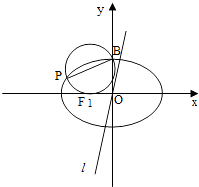
【解析】(1)设椭圆的右焦点为F2(c,0),由|AB|= ![]() |F1F2|.可得
|F1F2|.可得 ![]() ,再利用b2=a2﹣c2 , e=
,再利用b2=a2﹣c2 , e= ![]() 即可得出.(2)由(1)可得b2=c2 . 可设椭圆方程为
即可得出.(2)由(1)可得b2=c2 . 可设椭圆方程为 ![]() ,设P(x0 , y0),由F1(﹣c,0),B(0,c),可得
,设P(x0 , y0),由F1(﹣c,0),B(0,c),可得 ![]() ,
, ![]() .利用圆的性质可得
.利用圆的性质可得 ![]() ,于是
,于是 ![]() =0,得到x0+y0+c=0,由于点P在椭圆上,可得
=0,得到x0+y0+c=0,由于点P在椭圆上,可得 ![]() .联立可得
.联立可得 ![]() =0,解得P
=0,解得P ![]() .设圆心为T(x1 , y1),利用中点坐标公式可得T
.设圆心为T(x1 , y1),利用中点坐标公式可得T ![]() ,利用两点间的距离公式可得圆的半径r.设直线l的方程为:y=kx.利用直线与圆相切的性质即可得出.
,利用两点间的距离公式可得圆的半径r.设直线l的方程为:y=kx.利用直线与圆相切的性质即可得出.

 阅读快车系列答案
阅读快车系列答案【题目】某地区![]() 年至
年至![]() 年农村居民家庭纯收入
年农村居民家庭纯收入![]() (单位:千元)的数据如下表:
(单位:千元)的数据如下表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入 | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析![]() 年至
年至![]() 年该地区农村居民家庭人均纯收入的变化情况,并预测该地区
年该地区农村居民家庭人均纯收入的变化情况,并预测该地区![]() 年农村居民家庭人均纯收入.
年农村居民家庭人均纯收入.
![]() 注:
注: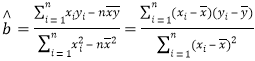 ,
,![]()
![]()