题目内容
【题目】如果存在常数a，使得数列{an}满足：若x是数列{an}中的一项，则a-x也是数列{an}中的一项，称数列{an}为“兑换数列”，常数a是它的“兑换系数”．
（1）若数列：2，3，6，m（m＞6）是“兑换系数”为a的“兑换数列”，求m和a的值；
（2）已知有穷等差数列{bn}的项数是n0（n0≥3），所有项之和是B，求证：数列{bn}是“兑换数列”，并用n0和B表示它的“兑换系数”；
（3）对于一个不少于3项，且各项皆为正整数的递增数列{cn}，是否有可能它既是等比数列，又是“兑换数列”？给出你的结论，并说明理由．
【答案】（1）a=9，m=7；（2）见解析；（3）见解析
【解析】
（1）利用“兑换数列”的定义得到a-m=2，a-6=3，即a=9，m=7．（2）利用“兑换数列”的定义可证明数列{bn}是“兑换数列”， 又因为数列{bn}所有项之和是B，所以B=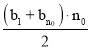
=
，即a=
；（3）假设存在这样的等比数列{cn}，设它的公比为q（q＞1），通过推理得到q=1，与q＞1矛盾，故不存在满足条件的数列{cn}．
（1）解：因为2，3，6，m（m＞6）是“兑换系数”为a的“兑换数列”
所以a-m，a-6，a-3，a-2也是该数列的项，且a-m＜a-6＜a-3＜a-2，
故a-m=2，a-6=3，即a=9，m=7．
（2）证明：设数列{bn}的公差为d，
因为数列{bn}是项数为n0项的有穷等差数列
若b1≤b2≤b3≤…≤
，则a-b1≥a-b2≥a-b3≥…≥a-，
即对数列{bn}中的任意一项bi（1≤i≤n0），a-bi=b1+（n0-i）d=+1-i∈{bn}
同理可得：b1≥b2≥b3≥…≥，a-bi=b1+（n0-i）d=+1-i∈{bn}也成立，
由“兑换数列”的定义可知，数列{bn}是“兑换数列”；
又因为数列{bn}所有项之和是B，所以B=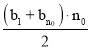=，即a=；
（3）解：假设存在这样的等比数列{cn}，设它的公比为q（q＞1），
因为数列{cn}为递增数列，所以c1＜c2＜c3＜…＜cn，则a-c1＞a-c2＞a-c3＞…＞a-cn，
又因为数列{cn}为“兑换数列”，则a-ci∈{cn}，所以a-ci是正整数
故数列{cn}必为有穷数列，不妨设项数为n项，则ci+cn+1-i=a（1≤i≤n）
①若n=3，则有c1+c3=a，c2=
，又c22=c1c3，由此得q=1，与q＞1矛盾
②若n≥4，由c1+cn=c2+cn-1，得c1-c1q+c1qn-1-c1qn-2=0
即（q-1）（1-qn-2）=0，故q=1，与q＞1矛盾；
综合①②得，不存在满足条件的数列{cn}．
