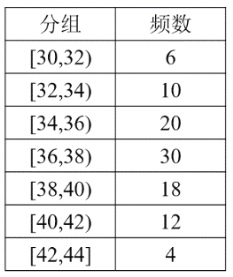
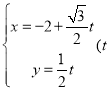题目内容
【题目】在如图所示的几何体中,EA⊥平面ABCD,四边形ABCD为等腰梯形,![]() ,且
,且![]() ,AD=AE=1,∠ABC=60°,EF=
,AD=AE=1,∠ABC=60°,EF=![]() AC,且EF
AC,且EF![]() AC.
AC.
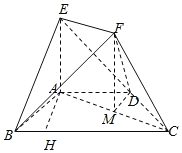
(Ⅰ)证明:AB⊥CF;
(Ⅱ)求二面角B﹣EF﹣D的余弦值.
【答案】(Ⅰ)见解析;(Ⅱ)![]()
【解析】
(Ⅰ)由EA⊥平面ABCD得BA⊥AE.由四边形ABCD为等腰梯形,![]() ,且
,且![]() ,∠ABC=60°,得AB⊥AC,进而推出AB⊥平面ACFE.即可得AB⊥CF.
,∠ABC=60°,得AB⊥AC,进而推出AB⊥平面ACFE.即可得AB⊥CF.
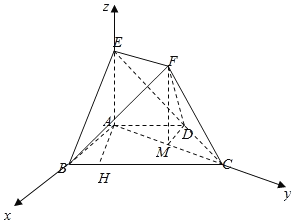
(Ⅱ)以A为坐标原点,AB,AC,AE分别为x,y,z轴,建立空间直角坐标系,求出平面BEF的一个法向量,平面DEF的一个法向量,通过向量的数量积求解二面角的余弦值即可.
(Ⅰ)由题知EA⊥平面ABCD,BA![]() 平面ABCD,∴BA⊥AE.
平面ABCD,∴BA⊥AE.
四边形ABCD为等腰梯形,![]() ,且
,且![]() ,AD=1,所以BC=2,∠ABC=60°,
,AD=1,所以BC=2,∠ABC=60°,
过点A作AH⊥BC于H,在RT△ABH中,![]() ,∴AB=1,
,∴AB=1,
在△ABC中,AC2=AB2+BC2﹣2ABBCcos60°=3,∴AB2+AC2=BC2,∴AB⊥AC,
且AC∩EA=A,∴AB⊥平面ACFE.又∵CF平面ACFE,∴AB⊥CF.
(Ⅱ)以A为坐标原点,AB,AC,AE分别为x,y,z轴,建立空间直角坐标系,
EF=![]() AC,且EF
AC,且EF![]() AC,AD=AE=1,则
AC,AD=AE=1,则 ,
,
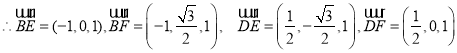
设![]() 为平面BEF的一个法向量,则
为平面BEF的一个法向量,则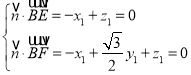 令
令![]() ,得
,得![]() ,
,
设![]() 为平面DEF的一个法向量,则
为平面DEF的一个法向量,则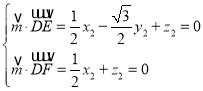 令
令![]() ,得
,得![]() ,
,
∴![]() ,二面角B﹣EF﹣D的余弦值为
,二面角B﹣EF﹣D的余弦值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目