题目内容
2.以椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为圆心的圆经过原点,且被椭圆的右准线分成弧长为2:1的两段弧,那么该椭圆的离心率等于( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 依据题意先求出椭圆的右焦点坐标、右准线方程,以及圆的半径,利用圆被椭圆的右准线分成弧长为2:1的两段弧,构造直角三角形,利用直角三角形中的边角关系求出离心率.
解答 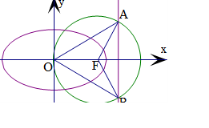 解:椭圆的右焦点F(c,0),右准线为x=$\frac{{a}^{2}}{c}$,圆的半径为c,
解:椭圆的右焦点F(c,0),右准线为x=$\frac{{a}^{2}}{c}$,圆的半径为c,
圆与右准线的两个交点A,D两点的横坐标为$\frac{{a}^{2}}{c}$,
∵圆被椭圆的右准线分成弧长为2:1的两段弧,∴∠AFD=120°,
∴△OAD是正三角形,由FA=FD,及∠AFD=120°,
构造直角三角形,利用边角关系得:
cos60°=$\frac{1}{2}$=$\frac{\frac{{a}^{2}}{c}-c}{c}$,
∴$\frac{{c}^{2}}{{a}^{2}}$=$\frac{2}{3}$,
∴e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$,
故选:B.
点评 本题考查椭圆的标准方程和简单性质,利用直角三角形中的边角关系求出离心率.

练习册系列答案
相关题目
16.在等比数列3,6,12,…中,第5项为( )
| A. | 18 | B. | 24 | C. | 36 | D. | 48 |
20.($\sqrt{x}-\frac{1}{x}$)9展开式中的常数项是( )
| A. | -36 | B. | 36 | C. | -84 | D. | 84 |
7.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的一个焦点为F,以F为圆心的圆与双曲线的两条渐近线分别相切于 A、B两点,且|AB|=$\sqrt{3}$b,则该双曲线的离心率为( )
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{{3\sqrt{5}}}{4}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{10}$ |
14.已知$M=\left\{{(x,y)\left|{y=\sqrt{1-{x^2}}}\right.}\right\}$,N={(x,y)|y=x+b},若M∩N≠∅,则实数b的范围是( )
| A. | [-1,1] | B. | $[{-\sqrt{2},1}]$ | C. | $[{-1,\sqrt{2}}]$ | D. | $[{-\sqrt{2},\sqrt{2}}]$ |
12.函数y=$\frac{1}{2}$(ex+e-x)的导数是( )
| A. | $\frac{1}{2}$(e x-e -x) | B. | $\frac{1}{2}$(e x+e -x) | C. | e x-e -x | D. | e x+e -x |
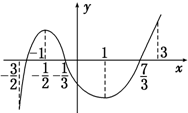 已知函数y=f(x)在定义域$({-\frac{3}{2},3})$上可导,其图象如图,记y=f(x)的导函数y=f′(x),则不等式xf′(x)≤0的解集是[0,1]∪(-$\frac{3}{2}$,-$\frac{1}{2}$].
已知函数y=f(x)在定义域$({-\frac{3}{2},3})$上可导,其图象如图,记y=f(x)的导函数y=f′(x),则不等式xf′(x)≤0的解集是[0,1]∪(-$\frac{3}{2}$,-$\frac{1}{2}$].