题目内容
15.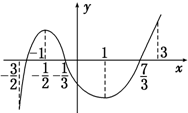 已知函数y=f(x)在定义域$({-\frac{3}{2},3})$上可导,其图象如图,记y=f(x)的导函数y=f′(x),则不等式xf′(x)≤0的解集是[0,1]∪(-$\frac{3}{2}$,-$\frac{1}{2}$].
已知函数y=f(x)在定义域$({-\frac{3}{2},3})$上可导,其图象如图,记y=f(x)的导函数y=f′(x),则不等式xf′(x)≤0的解集是[0,1]∪(-$\frac{3}{2}$,-$\frac{1}{2}$].
分析 由图象得到函数的单调区间,得到函数在个区间上导函数的符号,求出不等式的解.
解答 解:由f(x)的图象知x∈(-$\frac{3}{2}$,-$\frac{1}{2}$)时,递增,f′(x)>0;xf′(x)≤0?x≤0,
∴x∈(-$\frac{3}{2}$,-$\frac{1}{2}$)
x∈(-$\frac{1}{2}$,1)时,f(x)递减,f′(x)<0,∴xf′(x)≤0?x≥0,∴x∈[0,1]
x∈(1,3)时,f(x)递增,f′(x)>0,∴xf′(x)≤0?x≤0无解
故答案为:[0,1]∪(-$\frac{3}{2}$,-$\frac{1}{2}$].
点评 本题考查函数的单调性与导函数符号的关系:f′(x)>0则f(x)递增;f′(x)>0则f(x)递减.考查数形结合的数学数学方法.

练习册系列答案
相关题目
7.现有如下投资方案,一年后投资盈亏的情况如下:
(1)投资股市:
(2)购买基金:
(Ⅰ)已知甲、乙两人分别选择了“投资股市”和“购买基金”进行投资,如果一年后他们中至少有一人获利的概率大于$\frac{4}{5}$,求p的取值范围;
(Ⅱ)丙要将家中闲置的20万元钱进行投资,决定在“投资股市”、“购买基金”,或“等额同时投资股市和购买基金”这三种方案中选择一种,已知$p=\frac{1}{2}$,那么丙选择哪种投资方案,才能使得一年后投资收益的数学期望较大?(其中第三方案须考察两项获利之和的随机变量Z),给出结果并说明理由.
(1)投资股市:
| 投资结果 | 获利40% | 不赔不赚 | 亏损20% |
| 概 率 | $\frac{1}{2}$ | $\frac{1}{8}$ | $\frac{3}{8}$ |
| 投资结果 | 获利20% | 不赔不赚 | 亏损10% |
| 概 率 | p | $\frac{1}{3}$ | q |
(Ⅱ)丙要将家中闲置的20万元钱进行投资,决定在“投资股市”、“购买基金”,或“等额同时投资股市和购买基金”这三种方案中选择一种,已知$p=\frac{1}{2}$,那么丙选择哪种投资方案,才能使得一年后投资收益的数学期望较大?(其中第三方案须考察两项获利之和的随机变量Z),给出结果并说明理由.
2.以椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为圆心的圆经过原点,且被椭圆的右准线分成弧长为2:1的两段弧,那么该椭圆的离心率等于( )
| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{\sqrt{3}}{2}$ |
 已知函数f(x)=$\sqrt{3}sin2x-2{sin^2}$x+2,x∈R
已知函数f(x)=$\sqrt{3}sin2x-2{sin^2}$x+2,x∈R