题目内容
(本题满分12分)
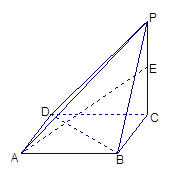
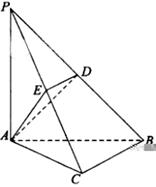
如图,在四棱锥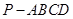 中,平面
中,平面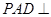 平面
平面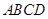 ,
,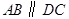 ,
,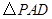 是等边三角形,已知
是等边三角形,已知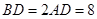 ,
,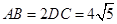 .
.
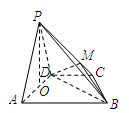
(Ⅰ)设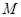 是
是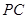 上的一点,证明:平面
上的一点,证明:平面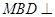 平面
平面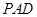 ;
;
(Ⅱ)求四棱锥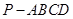 的体积.
的体积.
如图,在四棱锥
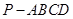 中,平面
中,平面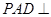 平面
平面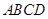 ,
,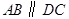 ,
,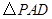 是等边三角形,已知
是等边三角形,已知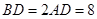 ,
,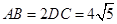 .
.
(Ⅰ)设
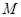 是
是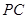 上的一点,证明:平面
上的一点,证明:平面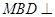 平面
平面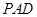 ;
;(Ⅱ)求四棱锥
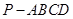 的体积.
的体积.(Ⅰ)由于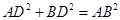 .故
.故 . 又平面
. 又平面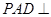 平面
平面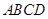 ,平面
,平面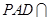 平面
平面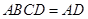 ,
,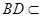 平面
平面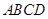 ,所以
,所以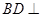 平面
平面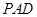 ,又
,又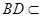 平面
平面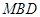 ,故平面
,故平面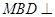 平面
平面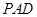 .
.
(Ⅱ)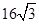 .
.
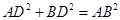 .故
.故 . 又平面
. 又平面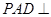 平面
平面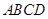 ,平面
,平面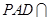 平面
平面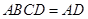 ,
,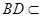 平面
平面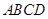 ,所以
,所以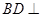 平面
平面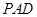 ,又
,又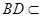 平面
平面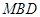 ,故平面
,故平面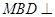 平面
平面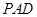 .
.(Ⅱ)
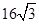 .
. 试题分析:(Ⅰ)由于
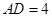 ,
,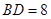 ,
,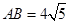 ,
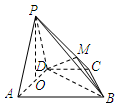
,所以
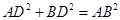 .
.故
 .
.
又平面
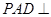 平面
平面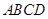 ,平面
,平面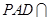 平面
平面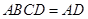 ,
,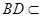 平面
平面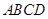 ,
,所以
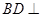 平面
平面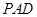 ,
,又
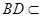 平面
平面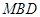 ,
,故平面
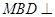 平面
平面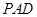 .
.(Ⅱ)解:过
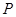 作
作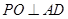 交
交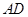 于
于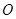 ,
,由于平面
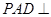 平面
平面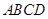 ,
,所以
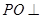 平面
平面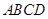 .
.因此
 为四棱锥
为四棱锥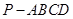 的高,
的高,又
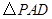 是边长为4的等边三角形.
是边长为4的等边三角形.因此
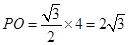 .
.在底面四边形
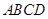 中,
中,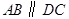 ,
,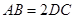 ,
,所以四边形
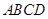 是梯形,在
是梯形,在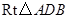 中,斜边
中,斜边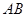 边上的高为
边上的高为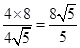 ,
,此即为梯形
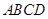 的高,
的高,所以四边形
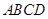 的面积为
的面积为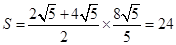 .
.故
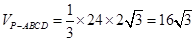 .
.点评:立体几何问题主要是探求和证明空间几何体中的平行和垂直关系以及空间角、体积等计算问题.对于平行和垂直问题的证明或探求,其关键是把线线、线面、面面之间的关系进行灵活的转化.在寻找解题思路时,不妨采用分析法,从要求证的结论逐步逆推到已知条件

练习册系列答案
相关题目
 和
和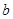 ,必定存在平面
,必定存在平面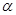 ,使得 ( )
,使得 ( )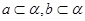
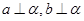
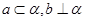
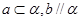
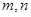 为两条不同的直线,
为两条不同的直线,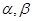 是两个不同的平面,下列命题正确的是
是两个不同的平面,下列命题正确的是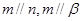 ,则
,则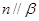
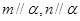 ,则
,则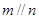
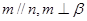 ,则
,则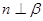
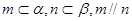 ,则
,则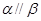
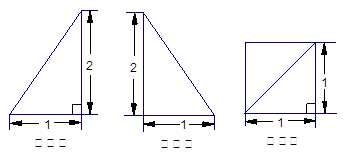
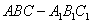 中,D是BC的中点,
中,D是BC的中点,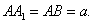
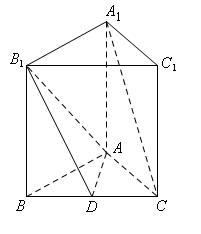
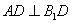 ;(Ⅱ)求证:
;(Ⅱ)求证: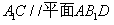 ;(Ⅲ)求三棱锥
;(Ⅲ)求三棱锥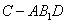 的体积.
的体积.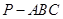 中,
中, ,
,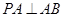 ,
,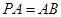 ,
,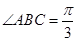 ,
,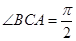 , 点
, 点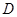 ,
, 分别在棱
分别在棱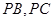 上,且
上,且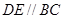 ,
,
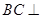 平面PAC
平面PAC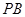 的中点时,求
的中点时,求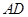 与平面
与平面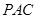 所成的角的正弦值;
所成的角的正弦值;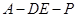 为直二面角?并说明理由.
为直二面角?并说明理由.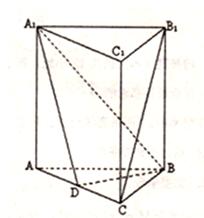
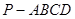 中,
中,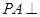 底面
底面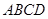 ,
,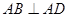 ,
,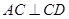 ,
,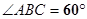 ,
,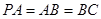 ,
,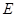 是
是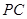 的中点.
的中点.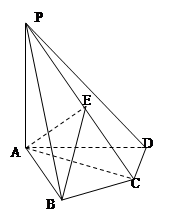
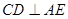 ;
;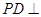 平面
平面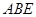 ;
;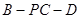 的余弦值.
的余弦值.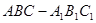 中, AC=4,CB=2,AA1=2,
中, AC=4,CB=2,AA1=2,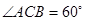 ,E、F分别是
,E、F分别是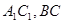 的中点。
的中点。
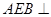 平面
平面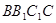 ;
;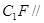 平面ABE;
平面ABE;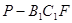 的体积。
的体积。