题目内容
(本题满分为12分)
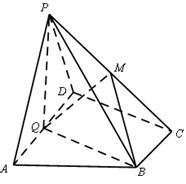
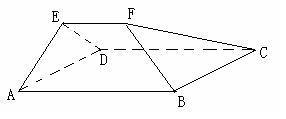
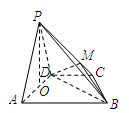
在四棱锥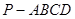 中,
中,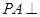 底面
底面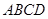 ,
,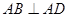 ,
,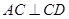 ,
,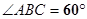 ,
,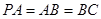 ,
,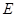 是
是 的中点.
的中点.
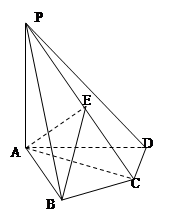
(I)证明: ;
;
(II)证明: 平面
平面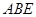 ;
;
(III)求二面角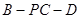 的余弦值.
的余弦值.
在四棱锥
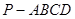 中,
中,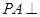 底面
底面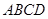 ,
,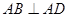 ,
,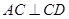 ,
,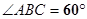 ,
, ,
, 是
是 的中点.
的中点.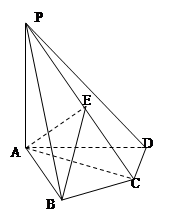
(I)证明:
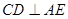 ;
;(II)证明:
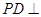 平面
平面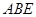 ;
;(III)求二面角
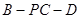 的余弦值.
的余弦值.(I)关键证明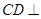 面
面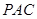 ,(II)
,(II)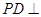 平面
平面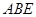 .(III)
.(III)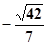
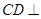 面
面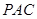 ,(II)
,(II)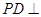 平面
平面 .(III)
.(III)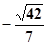
试题分析:(I)证明:
 底面
底面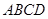 ,
,
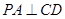 .又
.又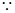
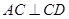

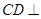 面
面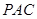 ,
,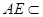 面
面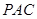 ,
,
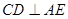 . (3分)
. (3分)(II)证明:
 ,
,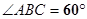

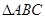 是等边三角形,
是等边三角形,
 ,又
,又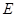 是
是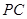 的中点,
的中点,
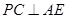 ,又由(1)可知
,又由(1)可知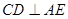 ,
,
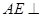 面
面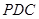

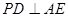
又
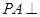 底面
底面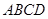 ,
,
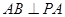 ,
,又
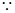
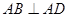

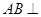 面
面

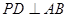

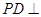 平面
平面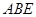 . (6分)
. (6分)(III)解:由题可知
 两两垂直,
两两垂直,如图建立空间直角坐标系,
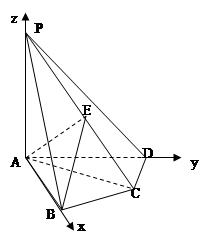
设
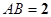 ,则
,则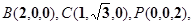
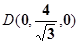 .
.设面
 的一个法向量为
的一个法向量为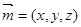
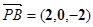
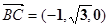
 即
即 取
取 则
则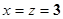 ,即
,即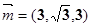
(9分)
设面
 的一个法向量为
的一个法向量为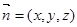
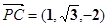
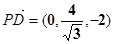
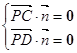 即
即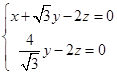 取
取 则
则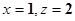 即
即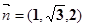
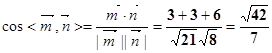
由图可知二面角
 的余弦值为
的余弦值为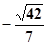 . (12分)
. (12分)点评:在立体几何中,证明直线与直线垂直、直线与平面垂直常用到直线与平面垂直的判定定理。另外,假如几何体是规则的图形,还是建立空间直角坐标系,用向量去解决问题较方便。

练习册系列答案
相关题目
 平面ABCD,EF∥AB, AB=2EF=2AD=4,
平面ABCD,EF∥AB, AB=2EF=2AD=4, .
.
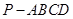 中,平面
中,平面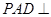 平面
平面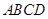 ,
,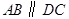 ,
,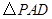 是等边三角形,已知
是等边三角形,已知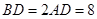 ,
,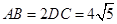 .
.
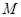 是
是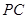 上的一点,证明:平面
上的一点,证明:平面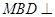 平面
平面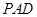 ;
;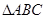 中,
中,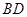 为
为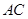 边上的高,
边上的高, ,沿
,沿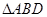 翻折,使得
翻折,使得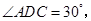 得几何体
得几何体

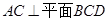 ;
;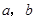 为两条直线,
为两条直线,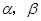 为两个平面,下列四个命题中,正确的命题是( )
为两个平面,下列四个命题中,正确的命题是( ) 所成的角相等,则
所成的角相等,则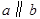
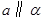 ,
,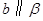 ,
,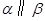 ,则
,则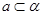 ,
,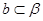 ,
,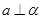 ,
,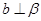 ,
, ,则
,则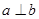
 AD=1,CD=
AD=1,CD=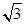 .
.