题目内容
对于两条不相交的空间直线 和
和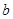 ,必定存在平面
,必定存在平面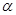 ,使得 ( )
,使得 ( )
 和
和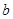 ,必定存在平面
,必定存在平面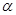 ,使得 ( )
,使得 ( )A.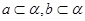 | B.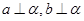 | C.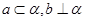 | D.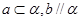 |
D
试题分析:∵空间直线a和b不相交
∴a、b的位置关系可能是平行或异面
再对各选项分别判断:
对于A,当a、b异面时,不存在平面
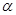 ,
,使a?α,b?α,故A不正确;
对于B,若要a⊥
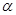 ,b⊥
,b⊥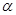 都成立,必须a、b互相平行,
都成立,必须a、b互相平行,所以当a、b不平行时,不存在平面
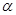 ,
,使a⊥
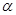 ,b⊥
,b⊥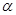 都成立,故B不正确;
都成立,故B不正确; 对于C,若要a?α,b⊥
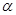 成立,必须a、b互相垂直,
成立,必须a、b互相垂直,也就是所成的角为90°时,才存在平面
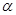 使a?α,b⊥
使a?α,b⊥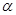 成立,
成立,但a、b平行或异面,异面时也不一定成90°角,故C不正确;
对于D,由于a、b的位置关系可能是平行或异面,
①当a、b平行时,很容易找到经过a的平面,但不经过b,可得b∥
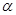 ;
;②当a、b异面时,可以在直线a上取一点O,经过O作直线c使c∥b,
设a、c确定的平面为
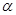 ,则直线a?α,b∥
,则直线a?α,b∥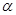 成立,
成立,综上所述,只有D项是正确的.
点评:本题借助于一个平面存在的问题,着重考查了平面的基本性质、直线与平面平行的判定定理和直线与平面垂直的定义与性质等知识点,属于基础题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
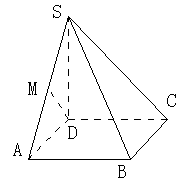
 的正方体
的正方体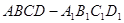 中,
中,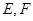 分别为
分别为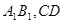 的中点.
的中点.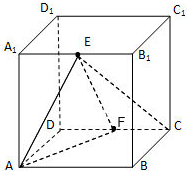
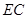 与平面
与平面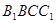 所 成 角的大小;
所 成 角的大小;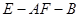 的大小.
的大小.

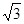 .
.
 SC;
SC;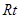 △ABC两直角边分别为3、4,PO⊥面ABC,O是△ABC的内心,PO=
△ABC两直角边分别为3、4,PO⊥面ABC,O是△ABC的内心,PO=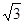 ,则点P 到△ABC的斜边AB的距离是( )
,则点P 到△ABC的斜边AB的距离是( ) 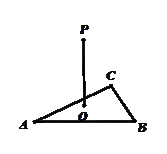
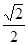
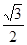
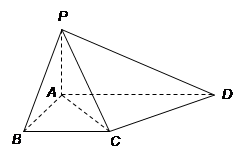
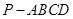 中,底面
中,底面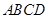 为直角梯形,且
为直角梯形,且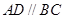 ,
,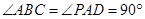 ,侧面
,侧面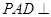 底面
底面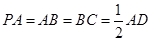 .
.
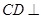 平面
平面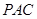 ;
;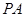 上是否存在点
上是否存在点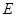 ,使得
,使得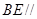 平面
平面 ?若存在,指出点
?若存在,指出点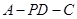 的余弦值.
的余弦值. 
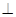 平面ABCD,EF∥AB, AB=2EF=2AD=4,
平面ABCD,EF∥AB, AB=2EF=2AD=4,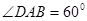 .
.
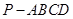 中,平面
中,平面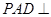 平面
平面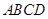 ,
,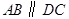 ,
,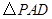 是等边三角形,已知
是等边三角形,已知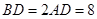 ,
,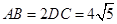 .
.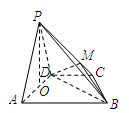
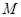 是
是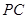 上的一点,证明:平面
上的一点,证明:平面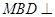 平面
平面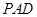 ;
;