题目内容
已知圆C：x2+（y-1）2=5，直线l：mx-y+1-m=0，m∈R．
（1）若直线l过圆C的圆心，求m的值；
（2）若直线l与圆C交于A，B两点，且|AB|=
，求直线l的倾斜角．
（1）若直线l过圆C的圆心，求m的值；
（2）若直线l与圆C交于A，B两点，且|AB|=
| 17 |
（1）圆心C（0，1），由C在直线l上，代入直线方程可得0-1+1-m=0，
解得：m=0．
（2）设d为圆心到直线的距离，则d=
，
由|AB|=2
=
，解得：m=±
，
而该直线的斜率为m，∴倾斜角α（α∈[0，π））的正切值tanα=±
，
∴α=
或α=
解得：m=0．
（2）设d为圆心到直线的距离，则d=
| |m| | ||
|
由|AB|=2
| r2-d2 |
| 17 |
| 3 |
而该直线的斜率为m，∴倾斜角α（α∈[0，π））的正切值tanα=±
| 3 |
∴α=
| π |
| 3 |
| 2π |
| 3 |
练习册系列答案
单元期中期末卷系列答案
相关题目
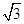，则a＝________.