Question

5．若集合A={x|$\sqrt{{x}^{2}-3}$=ax+1，x∈R}为空集，求实数a的取值范围．

Answer 1

分析 画出双曲线图象，利用直线系与双曲线的图形的关系，结合双曲线的性质，推出a的范围即可．

解答 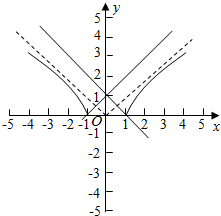解：集合A={x|$\sqrt{{x}^{2}-3}$=ax+1，x∈R}为空集，
就是y=$\sqrt{{x}^{2}-3}$与y=ax+1的图象没有交点，
如图：y=$\sqrt{{x}^{2}-3}$是双曲线的部分图象，渐近线的斜率为±1，
y=ax+1恒过（0，1），
函数的图象没有交点，可得a∈（-∞，-1）∪（1，+∞）．

点评 本题考查直线与双曲线的位置关系的综合应用，函数的零点问题，考查转化思想以及计算能力．