题目内容
15.集合A={x|-1≤x<3},B={x|2x-4≥x-2}(1)求A∩B:
(2)若集合C={x|2x+a>0}.满足B∪C=C.求实数a的取值范围.
分析 (1)化简B,根据集合的基本运算即可得到结论;
(2)化简C,利用B∪C=C,可得B⊆C,即可求实数a的取值范围.
解答 解:(1)∵A={x|-1≤x<3},B={x|2x-4≥x-2}={x|x≥2}.
∴A∩B={x|2≤x<3};
(2)C={x|2x+a>0}={x|x>-$\frac{1}{2}$a}.
∵B∪C=C,
∴B⊆C,
∴-$\frac{1}{2}$a<2,
∴a>-4.
点评 本题主要考查集合的基本运算,要求熟练掌握集合的交并运算,比较基础.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
5.设f(x)=2x+3,g(x)=f(x-2),则g(x)等于( )
| A. | 2x+1 | B. | 2x-1 | C. | 2x-3 | D. | 2x+7 |
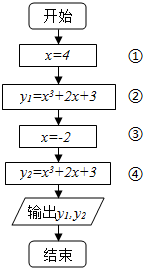 阅读如图所示的程序框图,回答下面的问题:
阅读如图所示的程序框图,回答下面的问题: