题目内容

14．求证：三角形的外心，重心，垂心在同一直线上．

分析 从三角形重心的唯一性入手，证明HO与中线BE的交点与重心G重合．

解答 证明：连接中位线DE（如图）．则DE∥AB，
又∵AH∥OD，BH∥OE（BH、OE同垂直于AC）．
故△DEO∽△ABH，
从而OE：HB=DE：AB=1：2．
连接OH交中线BE于G′．
∵BH∥OE，
∴△OEG′∽△HBG′．
因此，EG′：BG′=OE：HB=1：2．
这说明G′点即为△ABC的重心G．
从而H、G、O三点共线．

点评 此题主要考查了三角形中线的性质，以及三角形相似的性质，有一定综合性．

练习册系列答案
相关题目
4．对于命题：若O是线段AB上一点，则有|$\overrightarrow{OB}$|•$\overrightarrow{OA}$+|$\overrightarrow{OA}$|•$\overrightarrow{OB}$=$\overrightarrow{0}$．将它类比到平面的情形是：若O是△ABC内一点，则有S△OBC•$\overrightarrow{OA}$+S△OCA•$\overrightarrow{OB}$+S△OBA•$\overrightarrow{OC}$=$\overrightarrow{0}$，将它类比到空间情形应该是：若O是四面体ABCD内一点，则有VO-BCD•$\overrightarrow{OA}$+VO-ACD•$\overrightarrow{OB}$+VO-ABD•$\overrightarrow{OC}$+VO-ABC•$\overrightarrow{OD}$=$\overrightarrow{0}$．
5．若集合A={x|$\sqrt{{x}^{2}-3}$=ax+1，x∈R}为空集，求实数a的取值范围．
2．解不等式：||x|-|x-4||＞2．
9．已知sin（∂+θ）=$\frac{1}{2}$，sin（∂-θ）=$\frac{1}{3}$．证明：tan∂=5tanθ．
19．如图，球O中有一内接圆柱，当圆柱的体积最大时，圆柱的侧面积为16$\sqrt{2}$π，则球O的体积为32$\sqrt{3}$π
6．函数y=sinα（sinα-cosα）（α∈[-$\frac{π}{2}$，0]）的最大值为$\frac{1+\sqrt{2}}{2}$．
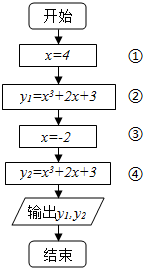3．阅读如图所示的程序框图，回答下面的问题：
（1）图框①中x=4的含义是什么？
（2）图框②中y1=x3+2x+3的含义是什么？
（3）图框④中y2=x3+2x+3的含义是什么？
（4）输出的y1和y2的值各为多少？
4．已知实数x、y、z不全为零，求证：$\sqrt{{x}^{2}+xy+{y}^{2}}$+$\sqrt{{y}^{2}+yz+{z}^{2}}$+$\sqrt{{z}^{2}+zx+{x}^{2}}$＞$\frac{3}{2}$（x+y+z）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网