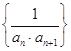题目内容
【题目】平面上有
个点，其中每两点之间的连线均染成红色或黑色.若图中总存在两个没有公共边的同色三角形，求的最小值.
【答案】8
【解析】
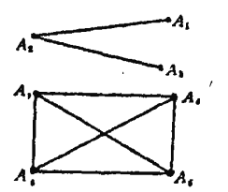
对于如图的七个点，并将图中的线画成红色，其余的线画成黑色.
于是图中
所得到的四个三角形，其中任何两个三角形都是有公共边的红色三角形.此外对四个黑三角形
，
也有一条公共边
，因此所求的最小正整数
.
下面证明
时符合题目要求，用反证法.
假设对8个点每两点的连线染成红、黑两色，但不满足题目要求.
由于对于6个点，则必存在一个单色三角形，不妨设
为红三角形（图中用实线连接）.
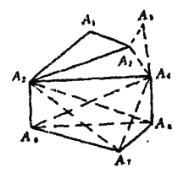
这时，考察除去
，
的其他6点.即
，
，…，
每两点连线染成二色的图形.由假设知，这6点存在的同色三角形只能是黑三角形，不妨设
是黑三角形（图中用虚线连接）.
再除去，，
的其余5点，由假设知这5点不能有单色三角形，于是只能为如图的情形，不妨设
所连线为红线，
所连线为黑线.
这时，再考察由，，，，
，这6点构成的图.由反证假设只能有两个红三角形，且这两个红三角形都以
为公共边，于是这两个三角形只能是
和
.所以
为红边，
为红边.类似地可证
和
为黑边，此时若
为红边则
与为无公共边红三角形，若为黑边，则
与
为无公共边黑三角形，均与反证假设矛盾.
综上，所求最小正整数为.
【题目】某电视台为宣传本省，随机对本省内15～65岁的人群抽取了
人，回答问题“本省内著名旅游景点有哪些”统计结果如图表所示.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 |
|
|
|
第2组 |
| 18 |
|
第3组 |
|
|
|
第4组 |
|
|
|
第5组 |
|
|
|
（1）分别求出
的值；
（2）从第2、3、4组回答正确的人中用分层抽样的方法抽取6人，求第2、3、4组每组各抽取多少人？
（3）指出直方图中，这组数据的中位数是多少（取整数值）？
【题目】汽车的普及给人们的出行带来了诸多方便，但汽车超速行驶也造成了诸多隐患.为了解汽车通过某一段公路时的车辆行驶情况，现随机抽测了通过这段公路的200辆汽车的行驶速度（单位：km/h），所得数据均在区间
内，其频率分布直方图如图所示.
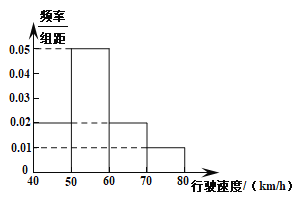
（1）求被抽测的200辆汽车的平均行驶速度.
（2）已知该路段属于事故高发路段，交警部门对此路段过往车辆限速60 km/h，并且对于超速行驶车辆有相应处罚：记分（扣除驾驶员驾照的分数）和罚款.
罚款情况如下：
超速情况 | 10%以内 | 10%~20% | 20%~50% | 50%以上 |
罚款情况 | 0元 | 100元 | 150元 | 500元 |
求被抽测的200辆汽车中超速10%~20%的车辆数.
