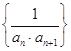题目内容
【题目】给定数列![]() . 对
. 对![]() ,该数列前
,该数列前![]() 项的最大值记为
项的最大值记为![]() ,后
,后![]() 项
项![]() 的最小值记为
的最小值记为![]() ,
,![]() .
.
(1)设数列![]() 为3,4,7,1. 写出
为3,4,7,1. 写出![]() 的值;
的值;
(2)设![]() 是公比大于
是公比大于![]() 的等比数列,且
的等比数列,且![]() ,证明
,证明![]() 是等比数列;
是等比数列;
(3)若![]() ,证明
,证明![]() 是常数列.
是常数列.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)见解析;(3)见解析
;(2)见解析;(3)见解析
【解析】
(1)根据![]() 的定义,求得
的定义,求得![]() 的值.
的值.
(2)根据数列![]() 的单调性,确定
的单调性,确定![]() ,根据等比数列的定义,证得
,根据等比数列的定义,证得![]() 是等比数列;
是等比数列;
(3)先证得![]() 后面的项,都不小于
后面的项,都不小于![]() ,然后证得
,然后证得![]() 后面的项,都不大于
后面的项,都不大于![]() ,由此证得
,由此证得![]() 后面的项,和
后面的项,和![]() 都相等,即证得数列
都相等,即证得数列![]() 的每一项和
的每一项和![]() 都相等,也即证得
都相等,也即证得![]() 是常数列.
是常数列.
(1)![]() ,
,![]() ,
,![]()
(2)因为![]() 是公比大于
是公比大于![]() 的等比数列,且
的等比数列,且![]()
所以![]() .
.
所以当![]() 时,
时,![]()
所以当![]() 时,
时,![]()
所以![]() 是等比数列.
是等比数列.
(3)因为![]() 即
即![]() ,故
,故![]() ,使
,使![]() ,且对
,且对![]() ,都有
,都有![]() ……①.
……①.
若![]() ,则
,则![]() ;
;
若![]() ,因为
,因为![]() ,所以
,所以![]()
![]() ,
,
所以对![]() ,都有
,都有![]() ……②.
……②.
由①②知,对![]() ,都有
,都有![]() .
.
综上,![]() .
.
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() ,使
,使![]() .
.
同上可证![]() .
.
以此类推,由于![]() 仅有有限项,所以
仅有有限项,所以![]() 是常数列.
是常数列.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
【题目】汽车的普及给人们的出行带来了诸多方便,但汽车超速行驶也造成了诸多隐患.为了解汽车通过某一段公路时的车辆行驶情况,现随机抽测了通过这段公路的200辆汽车的行驶速度(单位:km/h),所得数据均在区间![]() 内,其频率分布直方图如图所示.
内,其频率分布直方图如图所示.
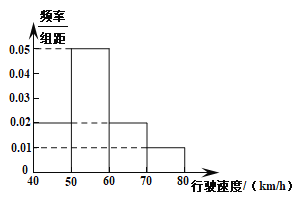
(1)求被抽测的200辆汽车的平均行驶速度.
(2)已知该路段属于事故高发路段,交警部门对此路段过往车辆限速60 km/h,并且对于超速行驶车辆有相应处罚:记分(扣除驾驶员驾照的分数)和罚款.
罚款情况如下:
超速情况 | 10%以内 | 10%~20% | 20%~50% | 50%以上 |
罚款情况 | 0元 | 100元 | 150元 | 500元 |
求被抽测的200辆汽车中超速10%~20%的车辆数.