题目内容
【题目】某工艺品厂要设计一个如图1所示的工艺品,现有某种型号的长方形材料如图2所示,其周长为4m,这种材料沿其对角线折叠后就出现图1的情况.如图,ABCD(AB>AD)为长方形的材料,沿AC折叠后AB'交DC于点P,设△ADP的面积为S2 , 折叠后重合部分△ACP的面积为S1 .
(Ⅰ)设AB=xm,用x表示图中DP的长度,并写出x的取值范围;
(Ⅱ)求面积S2最大时,应怎样设计材料的长和宽?
(Ⅲ)求面积(S1+2S2)最大时,应怎样设计材料的长和宽?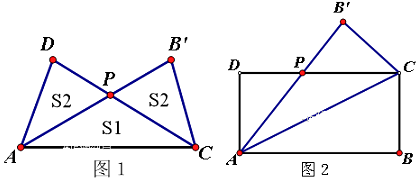
【答案】解:(Ⅰ)由题意,AB=x,BC=2﹣x,∵x>2﹣x,∴1<x<2
设DP=y,则PC=x﹣y,由△ADP≌△CB'P,故PA=PC=x﹣y,
由PA2=AD2+DP2,得(x﹣y)2=(2﹣x)2+y2
即: ![]() .
.
(Ⅱ)记△ADP的面积为S2,则 ![]() .
.
当且仅当 ![]() 时,S2取得最大值.
时,S2取得最大值.
故当材料长为 ![]() ,宽为
,宽为 ![]() 时,S2最大.
时,S2最大.
(Ⅲ) ![]()
于是令 ![]() ,∴
,∴ ![]()
∴关于x的函数 ![]() 在
在 ![]() 上递增,在
上递增,在 ![]() 上递减,
上递减,
∴当 ![]() 时,S1+2S2取得最大值.
时,S1+2S2取得最大值.
故当材料长为 ![]() ,宽为
,宽为 ![]() 时,S1+2S2最大
时,S1+2S2最大
【解析】(Ⅰ)设DP=y,根据图2将PC、AD用x,y表示,由图1可知![]() ,则PA=PC,在
,则PA=PC,在![]() 中,根据勾股定理列出等式;(Ⅱ)利用均值定理即可求解;(Ⅲ)构造函数F(t)=lnt-
中,根据勾股定理列出等式;(Ⅱ)利用均值定理即可求解;(Ⅲ)构造函数F(t)=lnt-![]() ,利用导数讨论函数F(t)的单调性.
,利用导数讨论函数F(t)的单调性.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目