题目内容
【题目】已知抛物线C:y2=4x的焦点为F,准线为l,P为C上一点,PQ垂直l于点Q,M,N分别为PQ,PF的中点,MN与x轴相交于点R,若∠NRF=60°,则|FR|等于( )
A.![]()
B.1
C.2
D.4
【答案】C
【解析】解:方法一:如图所示:连接MF,QF,
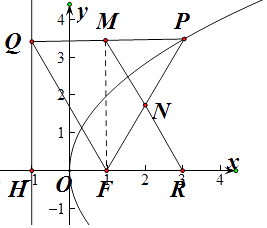
∵y2=4x的焦点为F,准线为l,P为C上一点
∴FH=2,PF=PQ
∵M,N分别为PQ,PF的中点,
∴MN∥QF,
∵PQ垂直l于点Q,
∴PQ∥OR,
∵PQ=PF,∠NRF=60°,
∴△PQF为等边三角形,
∴MF⊥PQ,
∴F为HR的中点,
∴FR=FH=2,
方法二:设P点的坐标为(x0,y0)
M,N分别为PQ,PF的中点,
∴MN∥QF,
∵∠NRF=60°,
∴∠QFH=60°,
∵∵y2=4x的焦点为F,准线为l,P为C上一点
∴FH=2,PF=PQ
∴QH=HFtan60°=2 ![]() ,
,
∵PQ垂直l于点Q
∴y0=2 ![]() ,
,
∴x0=3,
∴PQ=1+3=4,
∴QM=2,
∵四边形QMRF为平行四边形,
∴PR=QM=2
故选:C

练习册系列答案
相关题目


