题目内容
(本题满分12分)
已知椭圆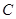 的两焦点是
的两焦点是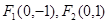 ,离心率
,离心率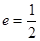 .
.
(Ⅰ)求椭圆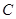 的方程;
的方程;
(Ⅱ)若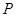 在椭圆
在椭圆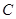 上,且
上,且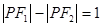 ,求DPF1F2的面积.
,求DPF1F2的面积.
(Ⅰ)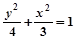 . (Ⅱ) S=
. (Ⅱ) S=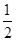 |PF1|×|PF2| sinÐF1PF2=
|PF1|×|PF2| sinÐF1PF2=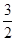 .
.
解析试题分析:(Ⅰ)由已知条件c=1, =
=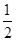 ,∴a=2,b=
,∴a=2,b= .……4分
.……4分
故椭圆方程为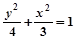 . ……
. ……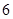 分
分
(Ⅱ)由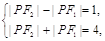

∴|PF1|=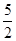 ,|PF2|=
,|PF2|=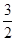 .……9分
.……9分
由余弦定理cosÐF1PF2=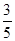 ,∴sinÐF1PF2=
,∴sinÐF1PF2=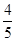 .
.
∴D F1PF2的面积为S=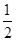 |PF1|×|PF2| sinÐF1PF2=
|PF1|×|PF2| sinÐF1PF2=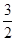 .……12分
.……12分
考点:本题主要考查椭圆的标准方程,椭圆的几何性质,余弦定理。
点评:基础题,涉及椭圆标准方程问题,要求熟练掌握a,b,c,e的关系,涉及“焦点三角形”问题,往往要利用椭圆的定义。

练习册系列答案
相关题目
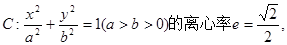 左、右焦点分别为F1、F2,点
左、右焦点分别为F1、F2,点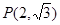 ,点F2在线段PF1的中垂线上。
,点F2在线段PF1的中垂线上。 与椭圆C交于M、N两点,直线F2M与F2N的倾斜角互补,求证:直线
与椭圆C交于M、N两点,直线F2M与F2N的倾斜角互补,求证:直线 过定点,并求该定点的坐标。
过定点,并求该定点的坐标。 与曲线
与曲线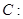

 交于不同的两点
交于不同的两点 ,
, 为坐标原点.
为坐标原点. ,求证:曲线
,求证:曲线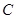 是一个圆;
是一个圆; ,当
,当 且
且 时,求曲线
时,求曲线 的取值范围.
的取值范围.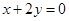 与圆
与圆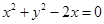 的交点为A、B,
的交点为A、B,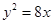 的焦点,M的离心率
的焦点,M的离心率 ,过M的右焦点F作不与坐标轴垂直的直线
,过M的右焦点F作不与坐标轴垂直的直线 ,交M于A,B两点。
,交M于A,B两点。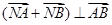 ,求实数t的取值范围。
,求实数t的取值范围。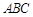 的两个顶点
的两个顶点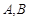 的坐标分别是
的坐标分别是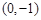 ,
,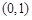 ,且
,且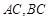 所在直线的斜率之积等于
所在直线的斜率之积等于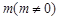 .
.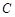 的轨迹
的轨迹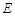 的方程,并判断轨迹
的方程,并判断轨迹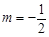 时,过点
时,过点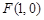 的直线
的直线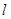 交曲线
交曲线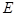 于
于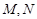 两点,设点
两点,设点 关于
关于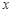 轴的对称点为
轴的对称点为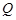 (
(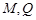 不重合).求证直线
不重合).求证直线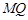 与
与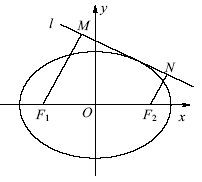
 的焦点与双曲线
的焦点与双曲线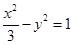 的右焦点重合.
的右焦点重合. 、
、 分别是椭圆
分别是椭圆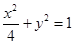 的左、右焦点。
的左、右焦点。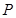 是第一象限内该椭圆上的一点,
是第一象限内该椭圆上的一点,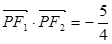 ,求点P的坐标;
,求点P的坐标; 与椭圆交于不同的两点A、B,且
与椭圆交于不同的两点A、B,且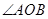 为锐角(其中
为锐角(其中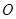 为坐标原点),求直线
为坐标原点),求直线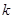 的取值范围。
的取值范围。