题目内容
(本大题满分14分)
已知△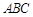 的两个顶点
的两个顶点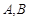 的坐标分别是
的坐标分别是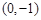 ,
,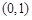 ,且
,且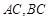 所在直线的斜率之积等于
所在直线的斜率之积等于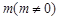 .
.
(Ⅰ)求顶点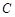 的轨迹
的轨迹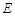 的方程,并判断轨迹
的方程,并判断轨迹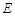 为何种圆锥曲线;
为何种圆锥曲线;
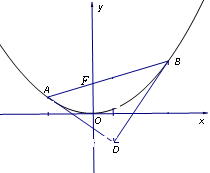
(Ⅱ)当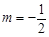 时,过点
时,过点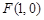 的直线
的直线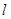 交曲线
交曲线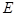 于
于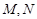 两点,设点
两点,设点 关于
关于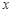 轴的对称点为
轴的对称点为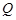 (
(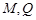 不重合).求证直线
不重合).求证直线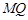 与
与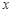 轴的交点为定点,并求出该定点的坐标.
轴的交点为定点,并求出该定点的坐标.
(1) (1) 当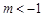 时 轨迹
时 轨迹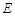 表示焦点在
表示焦点在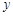 轴上的椭圆,且除去
轴上的椭圆,且除去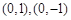 两点;
两点;
当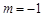 时 轨迹
时 轨迹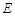 表示以
表示以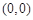 为圆心半径是1的圆,且除去
为圆心半径是1的圆,且除去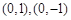 两点;
两点;
当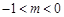 时 轨迹
时 轨迹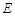 表示焦点在
表示焦点在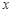 轴上的椭圆,且除去
轴上的椭圆,且除去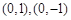 两点;
两点;
当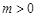 时 轨迹
时 轨迹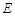 表示焦点在
表示焦点在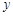 轴上的双曲线,且除去
轴上的双曲线,且除去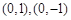 两点
两点
(2) 直线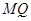 过定点
过定点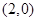
解析试题分析:(Ⅰ)由题知: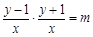
化简得: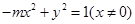 ……………………………2分
……………………………2分
当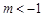 时 轨迹
时 轨迹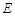 表示焦点在
表示焦点在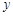 轴上的椭圆,且除去
轴上的椭圆,且除去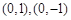 两点;
两点;
当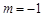 时 轨迹
时 轨迹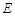 表示以
表示以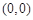 为圆心半径是1的圆,且除去
为圆心半径是1的圆,且除去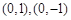 两点;
两点;
当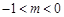 时 轨迹
时 轨迹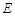 表示焦点在
表示焦点在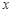 轴上的椭圆,且除去
轴上的椭圆,且除去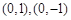 两点;
两点;
当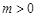 时 轨迹
时 轨迹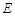 表示焦点在
表示焦点在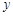 轴上的双曲线,且除去
轴上的双曲线,且除去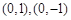 两点;
两点;
……………………………6分
(Ⅱ)设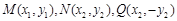
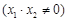
依题直线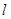 的斜率存在且不为零,则可设
的斜率存在且不为零,则可设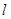 :
: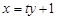 ,
,
代入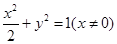 整理得
整理得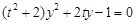
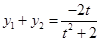 ,
,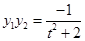 , ………………………………9分
, ………………………………9分
又因为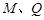 不重合,则
不重合,则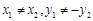

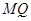 的方程为
的方程为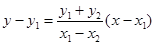 令
令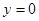 ,
,
得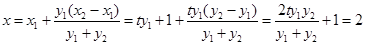
故直线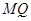 过定点
过定点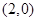 . ……………………………13分
. ……………………………13分
解二:设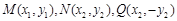
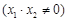
依题直线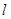 的斜率存在且不为零,可设
的斜率存在且不为零,可设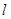 :
: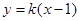
代入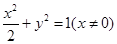 整理得:
整理得: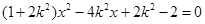
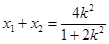 ,
,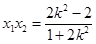 , ……………………………9分
, ……………………………9分
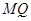 的方程为
的方程为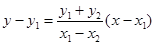 令
令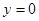 ,
,
得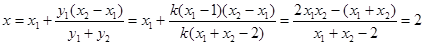
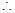 直线
直线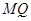 过定点
过定点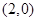 ……………………………13分
……………………………13分
考点:考查了圆锥曲线方程,以及直线与圆锥曲线的位置关系
点评:解决含参数的曲线方程的问题,主要是关注我们方程的特点来分类讨论得到,同时能结合设而不求的思想求解坐标,进而求解直线方程,属于中档题。

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
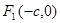 、
、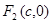 分别是椭圆
分别是椭圆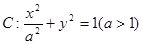 的左、右焦点,
的左、右焦点,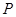 为椭圆
为椭圆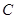 上任意一点,且
上任意一点,且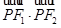 最小值为
最小值为 .
.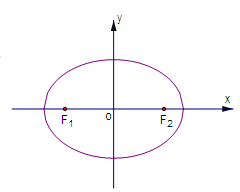
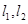 均与椭圆
均与椭圆 ,试探究在
,试探究在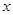 轴上是否存在定点
轴上是否存在定点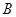 ,点
,点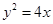 的焦点为
的焦点为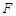 .过点
.过点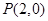 的直线交抛物线于
的直线交抛物线于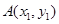 ,
,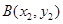 两点,直线
两点,直线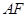 ,
,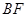 分别与抛物线交于点
分别与抛物线交于点 ,
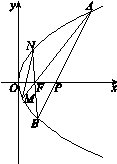
,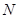 .
.
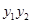 的值;
的值;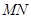 的斜率为
的斜率为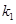 ,直线
,直线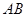 的斜率为
的斜率为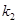 .证明:
.证明: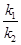 为定值.
为定值. 轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线
轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线 在
在 轴上的截距为
轴上的截距为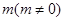 ,
,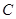 的两焦点是
的两焦点是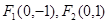 ,离心率
,离心率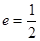 .
.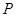 在椭圆
在椭圆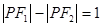 ,求DPF1F2的面积.
,求DPF1F2的面积.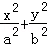 =1(a>b>0)的两个焦点分别为F1(﹣c,0),F2(c,0),M是椭圆短轴的一个端点,且满足
=1(a>b>0)的两个焦点分别为F1(﹣c,0),F2(c,0),M是椭圆短轴的一个端点,且满足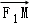
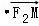 =0,点N( 0,3 )到椭圆上的点的最远距离为5
=0,点N( 0,3 )到椭圆上的点的最远距离为5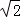
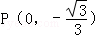 ;问A、B两点能否关于过点P、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
;问A、B两点能否关于过点P、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.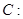
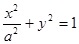 (
(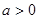 )的两个焦点是
)的两个焦点是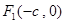 和
和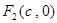 (
(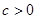 ),且椭圆
),且椭圆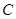 与圆
与圆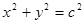 有公共点.
有公共点.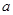 的取值范围;
的取值范围;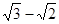 ,求椭圆的方程;
,求椭圆的方程;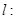
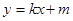 (
(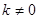 )与
)与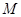 、
、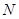 ,若线段
,若线段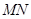 的垂直平分线恒过点
的垂直平分线恒过点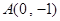 ,求实数
,求实数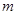 的取值范围.
的取值范围.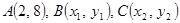 在抛物线
在抛物线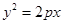 上,
上, 的重心与此抛物线的焦点F重合。
的重心与此抛物线的焦点F重合。 :
: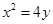 的焦点为
的焦点为 ,
, 、
、 是抛物线
是抛物线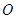 的不同两点,抛物线
的不同两点,抛物线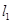 、
、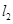 ,且
,且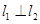 ,
, .
.