题目内容
9.已知函数f(x)=$\sqrt{3}$sin2x+cos2x,则( )| A. | f(x)(在(0,$\frac{π}{6}$)单调递增 | B. | f(x)在(-$\frac{π}{3}$,-$\frac{π}{6}$)单调递减 | ||
| C. | f(x)在(-$\frac{π}{6}$,0)单调递减 | D. | f(x)在($\frac{π}{6}$,$\frac{π}{3}$)单调递增 |
分析 先将函数整理为:f(x)=2sin(2x+$\frac{π}{6}$),得到关于x的不等式,解出即可.
解答 解:函数f(x)=$\sqrt{3}$sin2x+cos2x=2sin(2x+$\frac{π}{6}$),
∴由2kπ-$\frac{π}{2}$<2x+$\frac{π}{6}$<2kπ+$\frac{π}{2}$,解得:kπ-$\frac{2π}{3}$<x<kπ+$\frac{π}{6}$,
故选:A.
点评 本题考查了三角函数问题,考查函数的单调性问题,是一道基础题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
17.某种产品的广告费支出x与销售额(单位:百万元)之间有如下对应数据:
如果y与x之间具有线性相关关系.
(1)求这些数据的线性回归方程;
(2)预测当广告费支出为9百万元时的销售额.
附:线性回归方程$\widehaty=\widehatbx+\widehata$中,$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 50 | 60 | 70 |
(1)求这些数据的线性回归方程;
(2)预测当广告费支出为9百万元时的销售额.
附:线性回归方程$\widehaty=\widehatbx+\widehata$中,$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
14.已知函数f(x)=ex-1,g(x)=-x2+4x-3,若f(a)=g(b),则b的取值范围是( )
| A. | $[2-\sqrt{2},2+\sqrt{2}]$ | B. | $(2-\sqrt{2},2+\sqrt{2})$ | C. | [1,3] | D. | (1,3) |
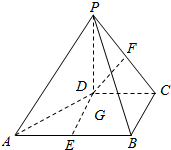 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=CB=1,BA=2,AB∥DC,∠BCD=90°,点E、F、G分别是线段AB、PC、DE的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=CB=1,BA=2,AB∥DC,∠BCD=90°,点E、F、G分别是线段AB、PC、DE的中点.